Riešené príklady > Vlnenie

269. Rušeň sa blíži k pozorovateľni rýchlosťou \( u = 20\,\mathrm{m \cdot s^{-1}} \).
Aký vysoký základný tón píšťaly počuje pozorovateľ, ktorý je v pokoji,
ak strojvodca počuje tón frekvencie \( f = 300\,\mathrm{s^{-1}} \)
a ak rýchlosť zvuku vo vzduchu za daných podmienok \( v_0 = 340\,\mathrm{m \cdot s^{-1}} \)?

\( u = 20\,\mathrm{m \cdot s^{-1}} \)

\( f = 300\,\mathrm{s^{-1}} \)

\( v_0 = 340\,\mathrm{m \cdot s^{-1}} = c \)

\( f^* = \,? \)

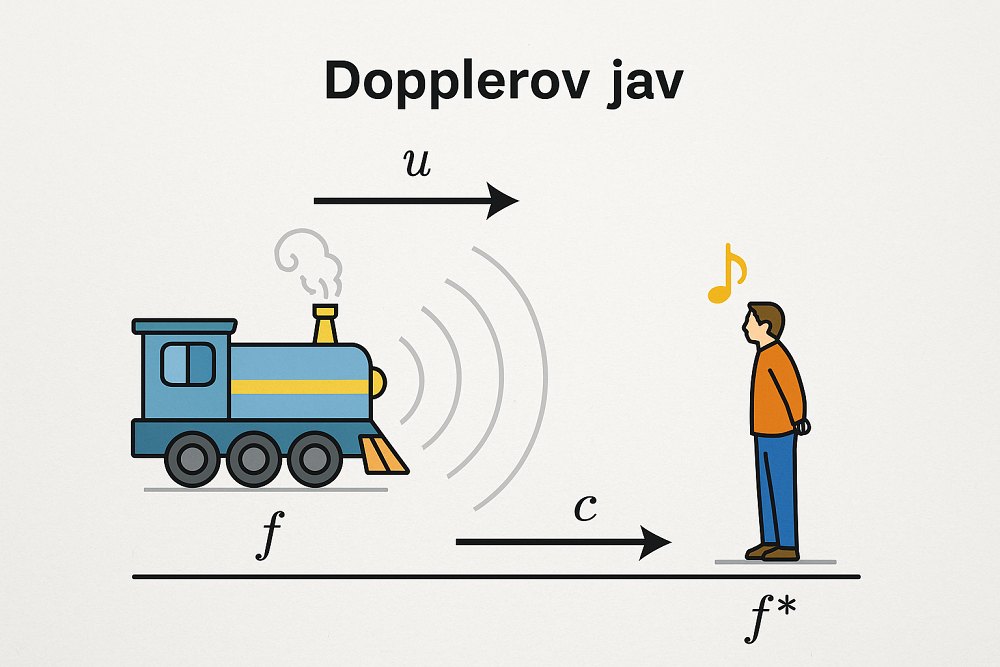
Zvuk je špeciálnym prípadom vlnenia, ktoré vnímame sluchom. Ak zdroj zvukových vĺn a pozorovateľ, ktorý ich vníma, sú v relatívnom pohybe, frekvencia zvuku sa pozorovateľovi javí iná ako v prípade, keby pozorovateľ a zdroj zvuku boli v relatívnom pokoji.
Ak sa pozorovateľ pohybuje vzhľadom na prostredie (vzduch, o ktorom predpokladáme, že je v pokoji) rýchlosťou \( v \) a zdroj rýchlosťou \( u \) v rovnakom smere, tak podľa Dopplerovho princípu súvis medzi frekvenciou \( f^* \), ktorú vníma pozorovateľ, a frekvenciou \( f \), ktorú by vnímal, keby bol vzhľadom na zdroj v pokoji, je daný vzťahom:

\[
f^* = \left( \frac{c - v}{c - u} \right) f \tag{1}
\]

kde \( c \) je rýchlosť zvuku vo vzduchu. Keď \( v < u \), potom \( f^* > f \).
Ak má rýchlosť v opačný smer ako \( u \), zdroj i pozorovateľ sa navzájom približujú. Potom platí:

\[
f^* = \left( \frac{c + v}{c - u} \right) f \tag{2}
\]

Zo zadania vyplýva, že rýchlosť pozorovateľa je \( v = 0\,\mathrm{m \cdot s^{-1}} \).
Potom pre hľadanú frekvenciu \( f^* \) platí:

\[
f^* = \left( \frac{c - v}{c - u} \right) f
\]

\[
f^* = \left( \frac{340\,\mathrm{m \cdot s^{-1}} - 0}{340\,\mathrm{m \cdot s^{-1}} - 20\,\mathrm{m \cdot s^{-1}}} \right) \cdot 300\,\mathrm{s^{-1}}
\]

\[
f^* = 318{,}75\,\mathrm{s^{-1}}
\]

Pozorovateľ počuje základný tón o frekvencii \( f^* = 318{,}75\,\mathrm{s^{-1}} \).