Riešené príklady > Termodynamika

399. Vypočítajte, ako sa zmení entropia ideálneho plynu teploty \( t_0 = 20\,^{\circ}\mathrm{C} \), tlaku \( p_0 = 0{,}1\,\mathrm{MPa} \) a objemu \( V_0 = 2\,\mathrm{l} \), keď sa rozopne do vákua na dvojnásobný objem \( 2V_0 \)!

\( t_0 = 20\,^{\circ}\mathrm{C} \;\Rightarrow\; T_0 = 293{,}15\,\mathrm{K}, \)
\( p_0 = 0{,}1\,\mathrm{MPa} = 10^5\,\mathrm{Pa}, \)
\( V_0 = 2\,\mathrm{l} = 2 \cdot 10^{-3}\,\mathrm{m^3}, \quad V = 2V_0, \)
\( \Delta S = \; ? \)

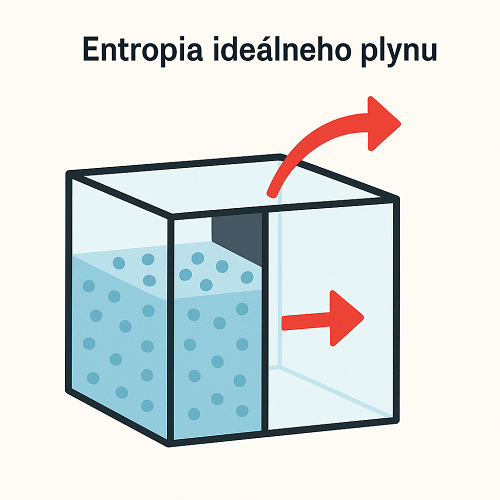
Po rozopnutí ideálneho plynu do vákua sa nemení ani jeho vnútorná energia, ani teplota, ako to dokazuje aj známy Gayov–Lussacov pokus. Keď sa plyn v začiatočnom stave vyznačoval entropiou \(S_0\) a v konečnom entropiou \(S_1\), pri zmene stavu sa jeho entropia zmenila o hodnotu:

\[ \Delta S = S_1 - S_0 \tag{1} \]

Pre túto zmenu entropie platí vzťah:

\[ \Delta S = \int \frac{\,\mathrm{d}Q\,}{T} \tag{2} \]

pričom \(\mathrm{d}Q\) predstavuje množstvo tepla, ktoré sústava vratným spôsobom naberie pri elementárnej stavovej zmene svojho stavu pri teplote \(T\). Z prvej vety termodynamickej pre ľubovoľné množstvo plynu platí:

\[ \mathrm{d}Q = \mathrm{d}U + \mathrm{d}A' \tag{3} \] \[ \mathrm{d}Q = n C_v \,\mathrm{d}T + p \,\mathrm{d}V \tag{4} \]

kde \(n\) je látkové množstvo, \(C_v\) mólová tepelná kapacita a \(p\) je tlak plynu, \(\mathrm{d}U\) predstavuje zmenu vnútornej energie pri elementárnej stavovej zmene, keď \(n\) mólov ideálneho plynu zmení teplotu o \(\mathrm{d}T\), a \(\mathrm{d}A'\) prácu, ktorú plyn vykoná pri elementárnej vratnej zmene svojho objemu o \(\mathrm{d}V\) proti vonkajším silám. Keďže teplota plynu sa nemení, \(\mathrm{d}T = 0\,\mathrm{K}\), aj zmena vnútornej energie \(\mathrm{d}U\) je nulová, takže pre zmenu entropie \(\Delta S\) ideálneho plynu platí:

\[ \Delta S = \int \frac{p\,\mathrm{d}V}{T} \tag{5} \]

Pre ľubovoľne zvolené množstvo plynu hmotnosti \(m\), ktorý obsahuje \(n = \frac{m}{M_m}\) mólov, môžeme písať stavovú rovnicu ideálneho plynu:

\[ pV = n R_m T \tag{6} \]

kde \(p\) je tlak zvoleného množstva plynu, \(T\) je termodynamická teplota. Po vyjadrení tlaku z predchádzajúcej rovnice (6) a dosadení do rovnice (5) dostaneme:

\[ \Delta S = n R_m \int \frac{\mathrm{d}V}{V} \tag{7} \] \[ \Delta S = n R_m \ln\!\left(\frac{V}{V_0}\right) \tag{8} \]

pričom sme integrovali v hraniciach od \(V_0\) po \(V\).

Z rovnice (6) si vyjadríme hodnotu \(nR_m\) pre plyn v počiatočnom stave:

\[ n R_m = \frac{p_0 V_0}{T_0} \tag{9} \]

a dosadíme do rovnice (8). Pre zmenu entropie ideálneho plynu platí:

\[ \Delta S = \frac{p_0 V_0}{T_0} \,\ln\!\left(\frac{V}{V_0}\right) \tag{10} \] \[ \Delta S = \frac{p_0 V_0}{T_0} \,\ln\!\left(\frac{2V_0}{V_0}\right) \tag{11} \] \[ \Delta S = \frac{p_0 V_0}{T_0} \,\ln 2 \tag{12} \]

Po dosadení číselných hodnôt dostaneme:

\[ \Delta S = \frac{\left(10^{5}\,\mathrm{Pa}\right)\,\left(2 \cdot 10^{-3}\,\mathrm{m^3}\right)} {293{,}15\,\mathrm{K}} \,\ln 2 \] \[ \Delta S = 0{,}473 \,\mathrm{J \cdot K^{-1}} \]

Entropia ideálneho plynu sa zmení o hodnotu \(0{,}473 \,\mathrm{J \cdot K^{-1}}\).