Riešené príklady > Termika

291. Homogénna železná tyč s hmotnosťou \( m = 3\,\mathrm{kg} \) má pri teplote \( 8\,^\circ\mathrm{C} \) dĺžku \( l = 1\,\mathrm{m} \).
Vypočítajte, ako sa zmení moment zotrvačnosti tejto tyče vzhľadom na os kolmú na smer tyče a prechádzajúcu jej koncovým bodom, keď sa zohreje na teplotu \( 100\,^\circ\mathrm{C} \).

\( m = 3\,\mathrm{kg},\quad l_1 = 1\,\mathrm{m} \)

\( t_1 = 8\,^\circ\mathrm{C},\quad t_2 = 100\,^\circ\mathrm{C} \)

\( \Delta t = 92\,^\circ\mathrm{C} \Rightarrow \Delta T = 92\,\mathrm{K} \)

\( \alpha = 12 \cdot 10^{-6}\,\mathrm{K^{-1}} \)

\( \Delta J = \,? \quad (\mathrm{kg \cdot m^2}) \)

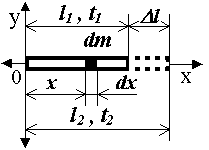
Moment zotrvačnosti homogénnej tyče vzhľadom na os prechádzajúcu jej koncovým bodom a kolmú na smer tyče vypočítame podľa vzťahu:

\[
J = \int x^2 \, \mathrm{d}m \tag{1}
\]

Keďže si element hmotnosti môžeme vyjadriť cez element dĺžky:

\[
\mathrm{d}m = \left( \frac{m}{l} \right) \mathrm{d}x \tag{2}
\]

potom pre moment zotrvačnosti tyče vzhľadom na danú os môžeme písať:

\[
J = \frac{m}{l} \int^l_0 x^2 \, \mathrm{d}x
\]

\[
J = \frac{m}{l} \left[ \frac{x^3}{3} \right]_0^l
\]

\[
J = \frac{1}{3} m l^2 \tag{3}
\]

Pre zmenu momentu zotrvačnosti po predĺžení tyče platí:

\[
\Delta J = J_2 - J_1 \tag{4}
\]

kde

\[
J_2 = \frac{1}{3} m l_2^2 \quad \text{a} \quad J_1 = \frac{1}{3} m l_1^2
\]

pričom

\[
l_2 = l_1 (1 + \alpha \Delta t) \tag{5}
\]

Využitím daných vzťahov pre zmenu momentu zotrvačnosti dostaneme:

\[
\Delta J = J_2 - J_1
\]

\[
\Delta J = \frac{1}{3} m l_1^2 \left( (1 + \alpha \Delta t)^2 - 1 \right)
\]

Po dosadení hodnôt zo zadania dostávame:

\[
\Delta J = \frac{1}{3} \cdot 3\,\mathrm{kg} \cdot (1\,\mathrm{m})^2 \cdot \left( (1 + 12 \cdot 10^{-6}\,\mathrm{K^{-1}} \cdot 92\,\mathrm{K})^2 - 1 \right)
\]

\[
\Delta J = 22 \cdot 10^{-4}\,\mathrm{kg \cdot m^2}
\]

Moment zotrvačnosti tyče vzhľadom na os kolmú na smer tyče a prechádzajúcu jej koncovým bodom sa po jej predĺžení zväčší približne o \( 22 \cdot 10^{-4}\,\mathrm{kg \cdot m^2} \).