Riešené príklady > Termika

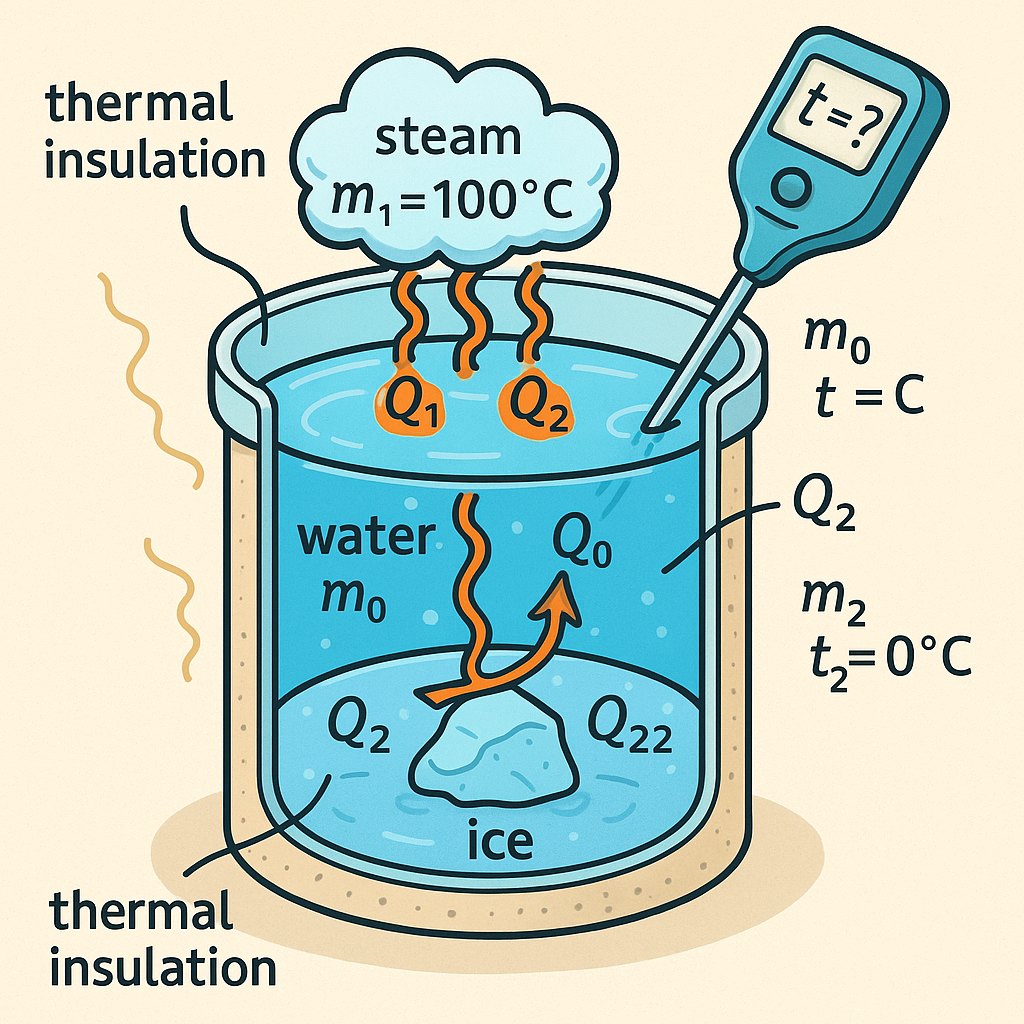
285. V tepelne izolovanej nádobe uvedieme do bezprostredného styku vodnú paru hmotnosti \( m_1 \) a teploty \( t_1 = 100\,^\circ\mathrm{C} \), vodu hmotnosti \( m_0 \) a teploty \( t_0 \) a ľad hmotnosti \( m_2 \) a teploty \( t_2 = 0\,^\circ\mathrm{C} \).
Po určitom čase – po skvapalnení zložiek – sa v nádobe vytvorí kvapalina.
Aká bude jej teplota?

Špecifické skupenské teplo varu vody je \( l_1 \),
topenia ľadu \( l_2 \)
a špecifická tepelná kapacita vody je \( c \).
Predpokladáme, že tepelnú kapacitu nádoby možno zanedbať.

\( m_1,\, m_0,\, m_2 \)

\( t_1 = 100\,^\circ\mathrm{C},\quad t_0,\quad t_2 = 0\,^\circ\mathrm{C} \)

\( l_1,\, l_2 \)

\( t = \,? \)

Pri riešení tohto príkladu si najprv musíme uvedomiť, aké zmeny v sústave nastanú,
kým sa obsah nádoby definitívne zmení na kvapalinu. Sú to tieto zmeny:

Vodná para teploty \( t_1 \) kondenzuje na vodu, pričom sa uvoľňuje teplo:

\[
Q_{1{,}1} = m_1 l_1 \tag{1}
\]

Táto voda má rovnakú teplotu ako para, z ktorej skondenzovala,
z čoho vyplýva, že ju ešte musí znížiť na výslednú teplotu sústavy \( t \),
a pritom uvoľniť teplo:

\[
Q_{1{,}2} = m_1 c (t_1 - t) \tag{2}
\]

Ľad teploty \( t_2 \) sa roztopí na vodu s rovnakou teplotou, pričom spotrebuje teplo:

\[
Q_{2{,}1} = m_2 l_2 \tag{3}
\]

Táto voda ešte musí zvýšiť svoju teplotu na výslednú teplotu sústavy \( t \) a pritom prijať teplo:

\[
Q_{2{,}2} = m_2 c (t - t_2) \tag{4}
\]

Voda teploty \( t_0 \) zmení svoju teplotu na výslednú teplotu sústavy \( t \), pričom spotrebuje teplo:

\[
Q_0 = m_0 c (t - t_0) \tag{5}
\]

Pretože uvažujeme o nádobe bez tepelnej kapacity,
musí platiť rovnosť medzi teplom získaným pri kondenzácii a ochladení pary
a teplom vydaným na skvapalnenie a zohriatie ľadu ako aj na zohriatie vody:

\[
Q_{1{,}1} + Q_{1{,}2} = Q_{2{,}1} + Q_{2{,}2} + Q_0 \tag{6}
\]

teda:

\[
m_1 l_1 + m_1 c (t_1 - t) = m_2 l_2 + m_2 c (t - t_2) + m_0 c (t - t_0)
\]

Po upravení dostávame vzťah pre výpočet výslednej teploty sústavy:

\[
t = \frac{m_1 c t_1 + m_2 c t_2 + m_0 c t_0 + m_1 l_1 - m_2 l_2}{m_1 c + m_2 c + m_0 c} \tag{7}
\]

Výsledná teplota sústavy sa vypočíta podľa vzťahu (7) po dosadení konkrétnych hodnôt.