Riešené príklady > Optika

908. Na doštičku z flintového skla dopadá svetlo pod uhlom \( \alpha = 56^\circ 12' \) a odráža sa ako úplne polarizované. Aký je index lomu skla?

\( \alpha = 56^\circ 12' \)
\( n = ? \)

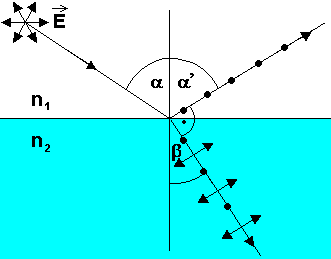
Keď absolútny index lomu vzduchu je \( n_{1} \) a absolútny index skla je \( n_{2} \) a platí podmienka, že odrazený lúč je úplne polarizovaný v rovine dopadu, pre uhol dopadu \( \alpha \) platí Brewsterov zákon:

\[ \tan \alpha = \frac{n_{2}}{n_{1}} \tag{1} \]

pričom pre uhol odrazu \( \alpha' \) podľa zákona odrazu platí \( \alpha' = \alpha \). (Odrazený lúč ostáva v rovine dopadu a uhol odrazu \( \alpha' \) sa rovná uhlu dopadu \( \alpha \).) Lomený lúč vnikajúci do skla pod uhlom \( \beta \) je polarizovaný čiastočne v rovine kolmej na rovinu dopadu a s odrazeným lúčom zviera uhol \( 90^\circ \). Index lomu skla \( n_{2} \) vypočítame úpravou vzťahu (1):

\[ n_{2} = n_{1} \, \tan \alpha \] \[ n_{2} = 1 \cdot \tan 56^\circ 12' \] \[ n_{2} = 1{,}1493 \] \[ n_{2} = 1{,}493 \]

Index lomu flintového skla, na ktoré dopadá svetlo pod uhlom \( 56^\circ 12' \), je \( 1{,}493 \).