Riešené príklady > Optika
Odraz a lom svetelného lúča
840. Pod akým uhlom má dopadnúť svetelný lúč na sklenú dosku s indexom lomu \( n_{2} = 1{,}57 \), aby odrazený a lomený lúč boli navzájom kolmé?
Keď svetelný lúč vniká do iného prostredia, ostáva v izotropnom prostredí v rovine dopadu, no od svojho pôvodného smeru sa odchýli. Keď \( \alpha \) je uhol dopadu a \( \beta \) uhol lomu svetelného lúča, podľa Snellovho zákona lomu podiel:
\[ \frac{\sin \alpha}{\sin \beta} = \frac{n_{2}}{n_{1}} = n \tag{1} \]
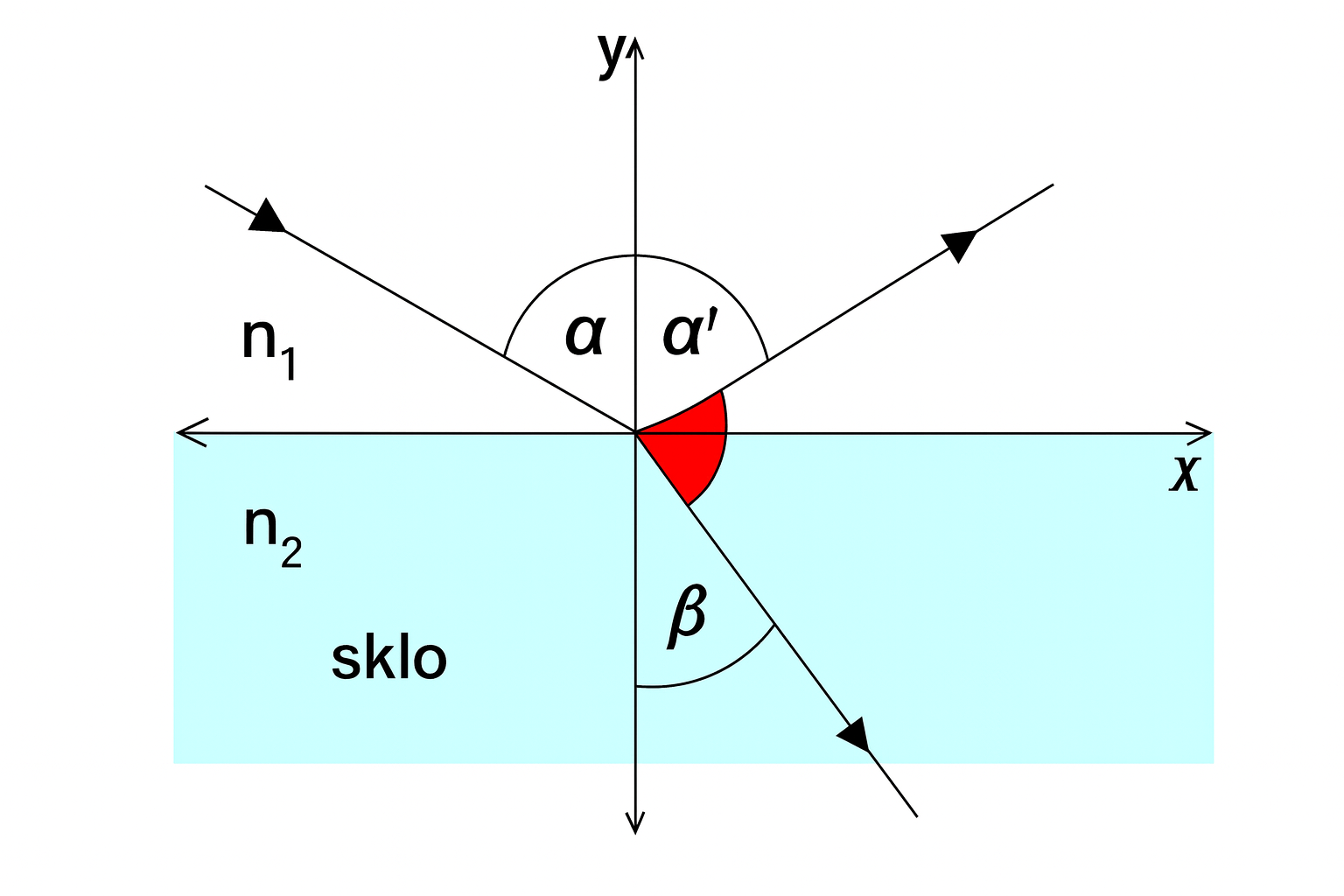
nezávisí od uhla dopadu a nazýva sa relatívny index lomu. Keďže odrazený a lomený lúč majú zvierať pravý uhol, potom (ako vidieť z obrázku) musí platiť:
\[ \alpha' + \beta + 90^\circ = 180^\circ \;\;\Rightarrow\;\; \beta = 90^\circ - \alpha' \tag{2} \]
Pretože podľa zákona odrazu uhol odrazu \( \alpha' \) sa rovná uhlu dopadu \( \alpha \):
\[ \alpha' = \alpha \tag{3} \]
zo vzťahu (2) vyplýva:
\[ \beta = 90^\circ - \alpha \tag{4} \]
Môžeme teda upraviť vzťah (1):
\[ \frac{\sin \alpha}{\sin \beta} = \frac{\sin \alpha}{\sin (90^\circ - \alpha')} = \frac{\sin \alpha}{\cos \alpha'} = \frac{\sin \alpha}{\cos \alpha} = \tan \alpha = n \tag{5} \]
odtiaľ pre hľadaný uhol \( \alpha \) platí:
\[ \alpha = \arctan n \] \[ \alpha = \arctan 1{,}57 \] \[ \alpha = 57^\circ 30' \tag{6} \]
Aby odrazený a lomený lúč boli navzájom kolmé, musí svetelný lúč dopadnúť pod uhlom \( \alpha = 57^\circ 30' \).