Riešené príklady > Kvapaliny

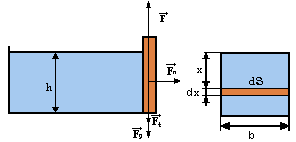
220. Aká sila je potrebná na zodvihnutie rovinnej hate, ktorá je pod tlakom vody, ak hmotnosť hate je \( 250\ \mathrm{kg} \), šírka je \( b = 3\ \mathrm{m} \), hĺbka vody je \( h = 1{,}5\ \mathrm{m} \) a koeficient trenia hate o opory je \( \mu = 0{,}3 \).

\( m = 250\ \mathrm{kg} \)

\( b = 3\ \mathrm{m} \)

\( \mu = 0{,}3 \)

\( F =\ ? \)

Aby sme zodvihli rovinnú hať, musíme prekonať pôsobenie tiažovej sily \( F_g \) na hať a vplyv trecej sily \( F_t \) hate o opory. Pre výslednú silu \( F \) teda platí:

\[ F = F_g + F_t \tag{1} \]

pričom veľkosti síl \( F_g \) a \( F_t \) si môžeme vyjadriť v tvare:

\[ F_g = mg \tag{2} \]

\[ F_t = \mu F_n \tag{3} \]

\( F_t \) predstavuje normálovú silu – silu kolmú na smer pohybu, a v tomto prípade je ňou hydrostatická tlaková sila. Keďže jej veľkosť sa počas zdvíhania hate v závislosti od tlaku vody mení, pre element veľkosti tejto sily v hĺbke \( x \), pôsobiacej na plochu \( dS \), môžeme písať:

\[ dF = p(x) \cdot dS \tag{4} \]

kde \( \rho \) predstavuje hustotu kvapaliny a hydrostatický tlak \( p \) v hĺbke \( x \) má veľkosť:

\[ p(x) = \rho g x \tag{5} \]

Veľkosť výslednej hydrostatickej tlakovej sily \( F_n \) určíme spočítaním jej elementov:

\[ F_n = \int_0^h \rho g x \cdot b \cdot dx = \rho g b \int_0^h x \, dx = \rho g b \cdot \frac{h^2}{2} \tag{6} \]

Z predchádzajúcich vzťahov vypočítame výslednú silu \( F \), ktorou budeme zdvíhať rovinnú hať:

\[ F = mg + \mu \cdot \frac{1}{2} \rho g b h^2 \tag{7} \]

Po dosadení zadaných hodnôt pre veľkosť výslednej sily \( F \) dostaneme:

\[ F = 250 \cdot 9{,}81 + \frac{1{,}5^2 \cdot 1000 \cdot 9{,}81 \cdot 3 \cdot 0{,}3}{2} \]

\[ F = 12\,385\ \mathrm{N} \]

Na zdvihnutie rovinnej hate, ktorá je pod tlakom vody, je potrebná sila \( 12\,385\ \mathrm{N} \).