Riešené príklady > Kmity
Tlmené harmonické kmity
Aký je koeficient útlmu tlmených harmonických kmitov hmotného bodu, keď podiel dvoch za sebou idúcich maximálnych výchyliek hmotného bodu na tú istú stranu sa rovná \( 2 \)
a perióda tlmených kmitov je \( T = 0{,}5\ \mathrm{s} \)?
Aká by bola perióda netlmených kmitov za rovnakých podmienok?
Skôr, ako začneme hľadať koeficient útlmu tlmených harmonických kmitov hmotného bodu \( b \),
vysvetlíme si pojmy útlm a logaritmický dekrement útlmu.
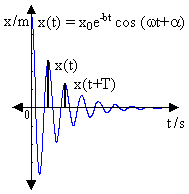
Útlm je definovaný ako podiel dvoch za sebou idúcich výchyliek na tú istú stranu, čiže:
\[
\lambda = \frac{x(t)}{x(t + T)} = \frac{x_0 e^{-b t} \cos(\omega t + \alpha)}{x_0 e^{-b (t + T)} \cos(\omega (t + T) + \alpha)} = e^{b T} \tag{1}
\]
kde b je hľadaný koeficient útlmu tlmených harmonických kmitov hmotného bodu. Logaritmický dekrement útlmu je prirodzený logaritmus útlmu, čiže:
\[
\delta = \ln \lambda = b T \tag{2}
\]
Odtiaľto pre koeficient útlmu tlmených harmonických kmitov hmotného bodu b platí
\[
b = \frac{\ln \lambda}{T} \tag{3}
\]
Zo zadania vyplýva, že útlm \( \lambda = 2 \) , takže:
\[
b = \frac{\ln 2}{T} \tag{4}
\]
Po dosadení za T = 0,5 s dostaneme:
\[
b = \frac{\ln 2}{0{,}5\,\text{s}} = 1{,}33\,\text{s}^{-1} \tag{5}
\]
Koeficient útlmu tlmených harmonických kmitov hmotného bodu je 1,33 s-1.
Pre uhlovú frekvenciu tlmených harmonických kmitov platí:
\[
\omega = \sqrt{\omega_0^2 - b^2} \tag{6}
\]
kde
\[
\omega_0 = \sqrt{\frac{k}{m}} \tag{7}
\]
je vlastná frekvencia netlmených harmonických kmitov. Pre periódu netlmených kmitov platí:
\[
T_0 = \frac{2\pi}{\omega_0} = \frac{2\pi}{\sqrt{\omega^2 + b^2}} = \frac{2\pi}{\sqrt{\left( \frac{2\pi}{T} \right)^2 + b^2}} \tag{8}
\]
čiže
\[
T_0 = 0{,}497\,\text{s}
\]