Riešené príklady > Kinematika
Zvislý vrh telies
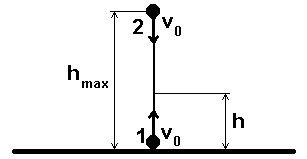
6. Teleso bolo vrhnuté zo zemského povrchu zvisle nahor rýchlosťou \(v_0 =4,9\,m.s^{-1} \). Súčasne z maximálnej výšky, ktorú toto teleso dosiahne, je vrhnuté zvisle nadol druhé teleso tou istou začiatočnou rýchlosťou \(v_0 \). Treba určiť čas \(t^* \), v ktorom sa obidve telesá stretnú, vzdialenosť \(h \) od zemského povrchu, v ktorej sa stretnú a rýchlosti obidvoch telies \(v1^*\) a \(v2^*\) v okamihu stretnutia. Odpor vzduchu zanedbajte!
Prvé teleso vrhnuté zvisle nahor sa pohybuje rovnomerne spomaleným pohybom. Pre jeho dráhu \( s_1 \) a rýchlosť \( v_1 \) platia vzťahy:
\[
s_1 = v_0 t - \frac{1}{2} g t^2 \tag{1}
\]
\[
v_1 = v_0 - g t \tag{2}
\]
kde \(\mathbf{s_1}\) je prejdená dráha v čase \(\mathbf{t}\), \(\mathbf{v_0}\) je počiatočná rýchlosť, \(\mathbf{v_1}\) rýchlosť telesa v čase \(\mathbf{t}\) a \(\mathbf{g}\) je tiažové zrýchlenie. Maximálnu výšku dosiahne prvé teleso v čase \(\mathbf{t_m}\) , v ktorom jeho rýchlosť \(\mathbf{v_1= 0 \, m.s^{-1}}\), takže zo vzťahu (2) vyplýva:
\[
t_m = \frac{v_0}{g}
\]
Zo vzťahu (1) dostaneme, že v čase tm prejde prvé teleso dráhu:
\[ h_{\max} = v_0 \left(\frac{v_0}{g}\right) - \frac{1}{2} g \left(\frac{v_0}{g}\right)^2 \]
\[ h_{\max} = \frac{1}{2} \frac{v_0^2}{g} \]
\[ s_2 = v_0 t + \frac{1}{2} g t^2 \tag{3} \]
\[ v_2 = v_0 + g t \tag{4} \]
kde s2 je prejdená dráha v čase t, v1 rýchlosť druhého telesa v čase t. V okamihu stretnutia oboch telies bude platiť:
\[
s_1 + s_2 = h_{\max} \tag{5}
\]
čiže:
\[
v_0 t^* - \frac{1}{2} g {t^*}^2 + v_0 t^* + \frac{1}{2} g {t^*}^2 = \frac{v_0^2}{2g}
\]
kde t* je čas, v ktorom sa telesá stretnú. Riešením predchádzajúcej rovnice dostaneme:
\[
2 v_0 t^* = \frac{v_0^2}{2g}
\]
\[
t^* = \frac{v_0}{4g}
\]
\[
t^* = \frac{4.9 \text{ m·s}^{-1}}{4 \cdot 9.81 \text{ m·s}^{-2}}
\]
\[
t^* = \underline{0.125 \text{ s}}
\]
Pre vzdialenosť h od zemského povrchu, v ktorej sa telesá stretnú platí:
\[
h = v_0 \left(\frac{v_0}{4g}\right) - \frac{1}{2} g \left(\frac{v_0}{4g}\right)^2
\]
\[
h = \frac{7 v_0^2}{32g}
\]
\[
h = \frac{7 \cdot 4.9^2 \text{ m}^2\text{s}^{-2}}{32 \cdot 9.81 \text{ m·s}^{-2}}
\]
\[
h = \underline{0.535 \text{ m}}
\]
Pre rýchlosti v1* a v2* v čase stretnutia t* dosadením do príslušných vzťahov dostaneme:
\[
v_1^* = v_0 - \frac{v_0}{4} = \frac{3v_0}{4}
\]
\[
v_1^* = \underline{3.675 \text{ m·s}^{-1}}
\]
\[
v_2^* = v_0 + \frac{v_0}{4} = \frac{5v_0}{4}
\]
\[
v_2^* = \underline{6.125 \text{ m·s}^{-1}}
\]
Obidve telesá sa stretnú za 0,125 s vo vzdialenosti 0,535 metra od zemského povrchu. V okamihu stretnutia budú mať telesá rýchlosti v1*= 3,675 m.s-1 a v2*= 6,125 m.s-1 .