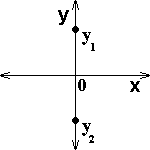Riešené príklady > Kinematika

36. Z určitej výšky sme súčasne tou istou začiatočnou rýchlosťou \(v_0\) hodili dve telesá; prvé zvislo nahor, druhé zvisle nadol. Ako závisí vzájomná vzdialenosť \(d\) týchto dvoch telies od času?

\(v_0\)

\(d = ? \) 

Zvoľme si súradnicovú sústavu tak, že smer nahor budeme považovať za kladný a smer nadol za záporný. Miesto, odkiaľ vyhadzujeme dve telesá, nech predstavuje počiatok súradnicovej sústavy. Teleso smerujúce nahor sa pohybuje rovnomerne spomaleným pohybom, teleso smerujúce nadol sa pohybuje rovnomerne zrýchleným pohybom. Pre súradnice telies v čase \(t\) platí:

\[ y_1 = v_0 t - \frac{1}{2} a t^2 \tag{1} \] \[ y_2 = -v_0 t - \frac{1}{2} a t^2 \tag{2} \]

pričom záporné znamienka súvisia s orientáciou vektorov rýchlosti a zrýchlenia smerom nadol. Zrýchlenie \(a\) je v homogénnom gravitačnom poli Zeme rovné \(g\). Vzájomnú vzdialenosť dvoch telies v čase \(t\) určíme ako rozdiel polôh oboch telies, čiže:

\[ d = y_1 - y_2 \] \[ d = v_0 t - \frac{1}{2} g t^2 - (-v_0 t - \frac{1}{2} g t^2) \] \[ d = v_0 t - \frac{1}{2} g t^2 + v_0 t + \frac{1}{2} g t^2 \] \[ d = 2 v_0 t \]

Vzájomná vzdialenosť dvoch telies v čase \(t\) je \(2 v_0 t\).