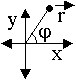Riešené príklady > Kinematika

27. Pohyb bodu je daný v polárnych súradniciach rovnicami \( r = n \cdot t \), \( \varphi = b \cdot t \), kde \( n \) a \( b \) sú konštanty.
Nájdite rovnicu dráhy pohybu a vyjadrite závislosť rýchlosti a zrýchlenia od času!

\( n \) , \( b \)

\( r = n \cdot t \)

\( v = ? \) , \( a = ? \)

Pohyb bodu je vyjadrený rovnicami:

\[ r = n t \tag{1} \]

\[ \varphi = b t \tag{2} \]

Keď si z predchádzajúcej rovnice (2) vyjadríme čas \( t \) a dosadíme do rovnice (1), dostaneme rovnicu dráhy pohybu bodu:

\[ r = \frac{n}{b} \varphi \tag{3} \]

Pohyb bodu v rovine možno okrem karteziánskych súradníc \( x, y \) opísať aj dvojicou krivočiarych - polárnych súradníc \( r, \varphi \). Medzi karteziánskymi a polárnymi súradnicami existuje vzájomne jednoznačné priradenie vyjadrené rovnicami:

\[ x = r \cos \varphi \tag{4} \]

\[ y = r \sin \varphi \tag{5} \]

pričom

\[ r = \sqrt{x^2 + y^2} \tag{6} \]

Dosadením pôvodných vzťahov \( r = n t \), \( \varphi = b t \) do predchádzajúcich rovníc (4) a (5) dostávame súradnice polohy bodu v čase \( t \):

\[ x = n t \cos b t \tag{7} \]

\[ y = n t \sin b t \tag{8} \]

Zderivovaním vzťahov (7), (8) podľa času dostaneme rovnice rýchlosti \( v_x \) a \( v_y \):

\[ v_x = \frac{dx}{dt} = n \cos b t + n t (-\sin b t) b \tag{9} \]

\[ v_y = \frac{dy}{dt} = n \sin b t + n t \cos b t b \tag{10} \]

Druhou deriváciou polohy bodu podľa času dostaneme vzťahy pre zrýchlenia \( a_x \), \( a_y \) v daných smeroch:

\[ a_x = \frac{d^2x}{dt^2} = n (-\sin b t) b + n (-\sin b t) b - n t \cos b t b^2 \tag{11} \]

\[ a_x = -2n \sin b t b - n t \cos b t b^2 \tag{12} \]

\[ a_y = \frac{d^2y}{dt^2} = n \cos b t b + n \cos b t b + n t (-\sin b t) b^2 \tag{13} \]

\[ a_y = 2n \cos b t b - n t \sin b t b^2 \tag{14} \]

Pre hodnotu celkovej rýchlosti \( v \) hmotného bodu platí:

\[ v = \sqrt{v_x^2 + v_y^2} \tag{15} \]

\[ v = \sqrt{[n \cos b t - n t \sin b t b]^2 + [n \sin b t + n t \cos b t b]^2} \]

\[ = \sqrt{(n \cos b t)^2 - 2n \cos b t n t \sin b t b + (n t \sin b t b)^2 + (n \sin b t)^2 + 2n \sin b t n t \cos b t b + (n t \cos b t b)^2} \]

\[ = \sqrt{(n \cos b t)^2 + (n t \sin b t b)^2 + (n \sin b t)^2 + (n t \cos b t b)^2} \]

\[ = \sqrt{n^2[\cos^2 b t + \sin^2 b t ] + n^2 t^2 b^2[\sin^2 b t + \cos^2 b t ]} \]

\[ = \sqrt{n^2 + n^2 t^2 b^2} = \sqrt{n^2(1+ t^2 b^2)} \]

\[ v = n \sqrt{1 + t^2 b^2} \tag{16} \]

Pre celkové zrýchlenie \( a \) platí:

\[ a = \sqrt{a_x^2 + a_y^2} \tag{17} \]

\[ a = \sqrt{[-2n \sin b t b - n t \cos b t b^2]^2 + [2n \cos b t b - n t \sin b t b^2]^2} \]

\[ = \sqrt{4n^2 \sin^2 b t b^2 + 4n \sin b t b n t \cos b t b^2 + n^2 t^2 \cos^2 b t b^4 + 4n^2 \cos^2 b t b^2 - 4n \cos b t b n t \sin b t b^2 + n^2 t^2 \sin^2 b t b^4} \]

\[ = \sqrt{4n^2 b^2[\cos^2 b t + \sin^2 b t] + n^2 t^2 b^4[\cos^2 b t + \sin^2 b t]} \]

\[ = \sqrt{4n^2 b^2 + n^2 t^2 b^4} = \sqrt{n^2 b^2(4 + t^2 b^2)} \]

\[ a = n b \sqrt{4 + t^2 b^2} \tag{18} \]

Dráha je Archimedova špirála s rovnicou:

\[ r = \frac{n}{b} \varphi \]

Rýchlosť bodu je

\[ v = n \sqrt{1 + t^2 b^2} \]

a jeho zrýchlenie

\[ a = n b \sqrt{4 + t^2 b^2} \]