Riešené príklady > Elektrina

559. Vypočítajte celkový náboj Zeme a plošnú hustotu náboja na jej povrchu, keď gradient potenciálu elektrického poľa zemského ovzdušia je na povrchu Zeme \(100 \ \text{V·m}^{-1}\) a keď polomer Zeme je \(6378 \ \text{km}\).

\( R = 6378 \ \text{km} = 6378000 \ \text{m}, \)
\( E = 100 \ \text{V·m}^{-1}, \)
\( \varepsilon_r = 1{,}00059, \)
\( \varepsilon_0 = 8{,}854 \cdot 10^{-12} \ \text{C}^2 \text{·N}^{-1} \text{·m}^{-2}, \)
\( Q, \ \sigma = ? \)

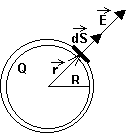
Zem s voľným nábojom \( Q \) je obklopená nekonečným plynným dielektrickým prostredím s relatívnou permitivitou \( \varepsilon_r \). Na dotykovej ploche vznikne v dôsledku polarizácie dielektrika viazaný náboj \( Q' \). Okolo Zeme s nábojom \( Q \) zostrojíme guľovú plochu \( S \) a počítame výtok elektrickej indukcie \( D \) z vnútra tejto plochy. Predpokladáme, že v dôsledku stredovej súmernosti Zeme má i jej pole rovnakú súmernosť a môžeme tvrdiť, že \( D \) má smer sprievodiča \( r \) a všade na guľovej ploche má rovnakú veľkosť. Potom zo zovšeobecnenej Gaussovej vety pre dielektrikum vyplýva: \[ \oint\limits_{S} \vec{D} \cdot d\vec{S} = Q \tag{1} \]

Tok vektora elektrickej indukcie \( \vec{D} \) ľubovoľnou uzavretou plochou sa rovná voľnému náboju, ktorý plocha uzatvára. (Tiež sa nazýva Maxwellov zákon.) Keďže indukcia elektrického poľa \( \vec{D} \) súvisí s intenzitou elektrického poľa \( \vec{E} \) vzťahom:

\[ \vec{D} = \varepsilon \vec{E} = \varepsilon_0 \varepsilon_r \vec{E} \tag{2} \]

úpravou zovšeobecnenej Gaussovej vety dostaneme:

\[ \oint\limits_{S} \vec{D} \cdot d\vec{S} = \oint\limits_{S} \varepsilon \vec{E} \cdot d\vec{S} = \varepsilon \oint\limits_{S} E \, dS = \varepsilon E \, 4 \pi r^{2} = Q \tag{3} \]

Pretože z vlastností skalárneho súčinu pre siločiary \( \vec{E} \) kolmé na plochu \( S \) vyplýva:

\[ \vec{E} \parallel d\vec{S} \;\;\Rightarrow\;\; \vec{E} \cdot d\vec{S} = E \, dS \tag{4} \]

Keďže pre veľkosť náboja \( dQ \) na povrchu elementárnej plochy \( dS \) Zeme platí:

\[ dQ = \sigma \, dS \tag{5} \]

Kde \( \sigma \) je plošná hustota elektrického náboja vo zvolenom bode plôšky \( dS \), môžeme využitím Gaussovej vety písať:

\[ \vec{E} \cdot d\vec{S} = E \, dS = \frac{dQ}{\varepsilon} = \frac{\sigma \, dS}{\varepsilon} \;\;\Rightarrow\;\; E = \frac{\sigma}{\varepsilon} \tag{6} \]

Z predchádzajúceho vzťahu vyplýva, že hľadanú plošnú hustotu náboja \( \sigma \) v danom mieste na povrchu Zeme môžeme vypočítať pomocou Coulombovej vety:

\[ \sigma = E \, \varepsilon \tag{7} \]

Ako súčin permitivity prostredia \( \varepsilon \) nachádzajúceho sa na povrchu Zeme a intenzity elektrického poľa \( E \) zadefinovanej ako gradient potenciálu \( \varphi \):

\[ \vec{E} = - \nabla \varphi \tag{8} \]

Porovnaním vzťahov (2) a (7) zistíme, že plošná hustota náboja \( \sigma \) predstavuje veľkosť vektora elektrickej indukcie \( \vec{D} \). Dosadením zadaných hodnôt do vzťahu (7) dostaneme:

\[ \sigma = E \, \varepsilon \] \[ \sigma = 100 \, \text{V·m}^{-1} \cdot 8{,}854 \cdot 10^{-12} \, \text{C}^2 \text{·N}^{-1} \text{·m}^{-2} \cdot 1{,}00059 \] \[ \sigma = 8{,}859 \cdot 10^{-10} \, \text{C·m}^{-2} \tag{9} \]

Keďže je elektrický náboj \( Q \) rozložený rovnomerne na guľovej ploche s polomerom \( R \), pole v mieste s polohovým vektorom \( r \) (pre \( r > R \)) je také isté ako v prípade bodového náboja uloženého v strede gule:

\[ \vec{E} = \int \frac{dQ}{4 \pi \varepsilon_0 \varepsilon_r} \, \frac{\vec{r}}{r^3} \tag{10} \]

Pričom \( dQ \) predstavuje náboj pripadajúci na element povrchu \( dS \). Vo vnútri gule (\( r < R \)) sa intenzita poľa rovná nule. Celkový náboj \( Q \) na povrchu Zeme určíme zo vzťahu (3) [prípadne zo vzťahu (10)], pričom pre polomer \( r \) guľovej plochy na jej povrchu platí \( r = R \):

\[ Q = E \, 4 \pi \varepsilon R^{2} \] \[ Q = 100 \cdot 4 \pi \cdot 8{,}854 \cdot 10^{-12} \cdot 1{,}00059 \cdot (6378000)^{2} \; \text{C} \] \[ Q = 4{,}529 \cdot 10^{5} \; \text{C} \tag{11} \]

Celkový náboj Zeme je \( 4{,}53 \cdot 10^{5} \ \text{C} \) a plošná hustota náboja na zemskom povrchu je \( 8{,}86 \cdot 10^{-10} \ \text{C·m}^{-2} \).