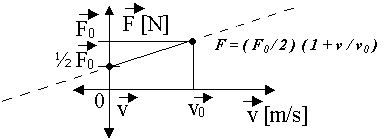Riešené príklady > Dynamika

74. Teleso hmotnosti \(m\) koná rovnomerný priamočiary pohyb rýchlosťou \(v_0\). Treba ho priviesť do pokoja brzdením na dráhe \(s_0\). Brzdiaca sila \(F\) postupne klesá lineárne s rýchlosťou, a to tak, že na konci pôsobenia, keď sa už teleso zastavilo, klesla hodnota sily na polovicu svojej pôvodnej hodnoty \(F_0\), ktorou sa vyznačovala na začiatku brzdenia. Určite hodnotu brzdiacej sily na začiatku brzdenia!

\(m, v_0 \)

\(F_0 = ? \)

Pre vyjadrenie závislosti \(F = F(v)\) si treba uvedomiť, že pri \(v = v_0\) sa \(F = F_0\) a pri \(v = 0 \, \text{m/s}\) sa \(F = \frac{F_0}{2}\). Týmto podmienkam, aj vzhľadom na znenie úlohy, vyhovuje vzťah:

\[ F = \frac{F_0}{2} \left(1 + \frac{v}{v_0} \right) \tag{1} \]

Keďže rýchlosť \(v\) telesa a brzdiaca sila \(F\) spadajú do tej istej priamky, ale majú opačný smer, pohybová rovnica telesa bude mať tvar:

\[ m \frac{dv}{dt} = - \frac{F_0}{2} \left(1 + \frac{v}{v_0} \right) \tag{2} \]

Keďže \(ds = v \, dt\), teda \(dt = \frac{ds}{v}\), možno rovnicu (2) upraviť na tvar:

\[ m v \frac{dv}{ds} = - \frac{F_0}{2} \left(1 + \frac{v}{v_0} \right) \tag{3} \] \[ ds = - \frac{2m}{F_0} \cdot \frac{v \, dv}{1 + \frac{v}{v_0}} \tag{4} \]

Predchádzajúcu rovnicu integrujeme od začiatku brzdenia \(v = v_0\) až do zastavenia telesa \(v = 0 \, \text{m/s}\). Dostaneme:

\[ s_0 = \frac{2m v_0}{F_0} \left[ v - v_0 \ln(v + v_0) \right] \bigg|_0^{v_0} \tag{5} \] \[ s_0 = \frac{2m v_0^2}{F_0} \left(1 - \ln 2 \right) \tag{6} \]

Pre silu \(F_0\) platí:

\[ F_0 = \frac{2m v_0^2}{s_0 (1 - \ln 2)} \tag{7} \]

Vzťah pre hodnotu brzdiacej sily \(F_0\) na začiatku brzdenia vyjadruje rovnica (7).