Zadania príkladov

(1.) Úsečka AB konštantnej dĺžky sa pohybuje tak, že jej koncové body A, resp. B kĺžu pozdĺž osi \(y\), resp. osi \(x\) určitej pravouhlej súradnicovej sústavy. Treba určiť, akú dráhu bude pri tomto pohybe opisovať ľubovoľne zvolený bod M na uvedenej úsečke AB.
[Bod M sa pohybuje po elipse s polosami \(a, b\).]

(6.) Teleso bolo vrhnuté zo zemského povrchu zvisle nahor rýchlosťou \(v_0 = 4{,}9 \,\text{m·s}^{-1}\). Súčasne z maximálnej výšky, ktorú toto teleso dosiahne, je vrhnuté zvisle nadol druhé teleso tou istou začiatočnou rýchlosťou \(v_0\). Treba určiť čas \(t^*\), v ktorom sa obidve telesá stretnú, vzdialenosť \(h\) od zemského povrchu, v ktorej sa stretnú a rýchlosti obidvoch telies \(v_1^*\) a \(v_2^*\) v okamihu stretnutia. Odpor vzduchu zanedbajte!
[\(t = 0{,}125 \,\text{s};\; d = 0{,}535 \,\text{m}\) od zemského povrchu; \(v_1^* = 3{,}675 \,\text{m·s}^{-1},\; v_2^* = 6{,}125 \,\text{m·s}^{-1}\)]

(9.) Cyklista sa pohybuje smerom do kopca konštantnou rýchlosťou \(v_1 = 10 \,\text{km·h}^{-1}\). Keď dosiahne vrchol kopca, obráti sa a absolvuje tú istú trať z kopca dolu rýchlosťou \(v_2 = 40 \,\text{km·h}^{-1}\). Aká je priemerná rýchlosť pohybu cyklistu?
[\(v_p = 16 \,\text{km·h}^{-1}\)]

(27.) [1.47] Pohyb bodu je daný v polárnych súradniciach rovnicami \(r = nt,\; \varphi = bt\), kde \(n\) a \(b\) sú konštanty. Nájdite rovnicu dráhy pohybu a vyjadrite závislosť rýchlosti a zrýchlenia od času!
[Dráha je Archimedova špirála s rovnicou \(r = \tfrac{n}{b} \varphi;\; v = n \sqrt{1 + b^2t^2};\; a = nb \sqrt{4 + b^2t^2}\)]

(33.) [1.16] Pozorovateľ stojaci v okamihu rozbehu vlaku pri jeho začiatku zaznamenal, že prvý vagón prešiel popri ňom za čas \(t_1 = 4 \,\text{s}\). Ako dlho bude popri ňom prechádzať \(n\)-tý vagón (napr. \(n = 7\)), keď všetky vagóny sú rovnako dlhé? Pohyb vlaku považujte za priamočiary, rovnomerne zrýchlený.
[\(t^* = t_1(\sqrt{n} - \sqrt{n-1}) = t_1(\sqrt{7} - \sqrt{6}) = 0{,}8 \,\text{s}\)]

(47.) Aká je priemerná rýchlosť pohybu automobilu v prípade, že:
a) prvú polovicu času svojho pohybu sa pohybuje rýchlosťou \(v_1 = 100 \,\text{km·h}^{-1}\) a druhú polovicu času sa pohybuje rýchlosťou \(v_2 = 60 \,\text{km·h}^{-1}\);
b) polovicu z celkovej svojej dráhy prejde rýchlosťou \(v_1 = 100 \,\text{km·h}^{-1}\) a druhú polovicu dráhy rýchlosťou \(v_2 = 60 \,\text{km·h}^{-1}\)?
[a) \(v_p = 80 \,\text{km·h}^{-1}\); b) \(v_p = 75 \,\text{km·h}^{-1}\)]

(53.) Hmotný bod koná pohyb po kružnici s polomerom \(R = 20 \,\text{cm}\) so stálym uhlovým zrýchlením \(\varepsilon = 2 \,\text{s}^{-2}\). Vypočítajte hodnotu tangenciálneho, normálového a celkového zrýchlenia na konci 4-tej sekundy od začiatku pohybu, keď v čase \(t = 0 \,\text{s}\) bol hmotný bod v pokoji!
[\(a_t = 40 \,\text{cm·s}^{-2};\; a_n = 1280 \,\text{cm·s}^{-2};\; a = 1280{,}6 \,\text{cm·s}^{-2}\)]

(54.) Po opustení stanice rýchlosť vlaku rovnomerne narastá a po troch minútach od opustenia stanice dosahuje na dráhe zakrivenej do tvaru kružnice s polomerom \(R = 800 \,\text{m}\) hodnotu \(72 \,\text{km·h}^{-1}\). Treba určiť hodnotu tangenciálneho, normálového a celkového zrýchlenia po dvoch minútach od okamihu opustenia stanice.
[\(a_t = 0{,}111 \,\text{m·s}^{-2};\; a_n = 0{,}222 \,\text{m·s}^{-2};\; a = 0{,}248 \,\text{m·s}^{-2}\)]

(56.) Koleso sa z pokojového stavu dáva do otáčavého pohybu so stálym uhlovým zrýchlením \(\varepsilon = 2 \,\text{s}^{-2}\). Koľkokrát sa otočí za prvých 15 sekúnd svojho otáčania?
[\(N = 35{,}8\)]

(61.) Bod M sa pohybuje z vrcholu kužeľa rovnomerne priamočiaro rýchlosťou veľkosti \(c\) po jeho povrchovej priamke. Kužeľ sa otáča okolo svojej osi stálou uhlovou rýchlosťou veľkosti \(\omega\). Vypočítajte absolútne zrýchlenie bodu M v čase \(t\) od začiatku pohybu, keď uhol medzi osou kužeľa a povrchovou priamkou je \(\alpha\)!
[\(a = \omega c \sin \alpha \sqrt{\omega^2 t^2 + 4}\)]

(63.) Tyč OA sa otáča okolo osi kolmej na tyč a prechádzajúcej bodom O tyče konštantnou uhlovou rýchlosťou \(\omega\). Bod M sa pohybuje v smere tejto tyče konštantnou rýchlosťou \(v'\). Vypočítajte veľkosť absolútneho zrýchlenia bodu M!
[\(a = \omega \sqrt{r'^2 \omega^2 + 4 v'^2}\)]

(99.) Železničný vozeň sa pohybuje po vodorovnej priamej trati a brzdíme ho silou, ktorá sa rovná \(0{,}1\) tiaže vozňa. Vypočítajte čas meraný od začiatku brzdenia, za ktorý vozeň zastaví, ako aj dráhu, ktorú od začiatku brzdenia až do zastavenia prejde, ak v okamihu, keď sa začalo brzdiť, mal vozeň rýchlosť \(v_0 = 72 \,\text{km·h}^{-1}\)! [\(t = 20{,}4 \,\text{s};\; s = 204 \,\text{m}\)]

(102.) Guľôčka s hmotnosťou \(m\), ktorej bola udelená začiatočná rýchlosť \(v_0\), sa pohybuje v prostredí, ktorého odpor \(F\) proti jej pohybu rastie lineárne s rýchlosťou hmotného bodu, t.j. \(F = - kv\). Akú dráhu až do zastavenia guľôčka prejde, keď okrem odporu prostredia nepôsobí na ňu žiadna sila? [\(s = \tfrac{m v_0}{k}\)]

(106.) Motor auta celkovej hmotnosti \(960 \,\text{kg}\) má ťažnú silu \(1600 \,\text{N}\). Za koľko sekúnd môže auto dosiahnuť rýchlosť \(v = 54 \,\text{km·h}^{-1}\)? [\(t = 9 \,\text{s}\)]

(109.) Oceľová špirála dĺžky \(l_0 = 80 \,\text{cm}\) sa predĺži silou \(F_1 = 20 \,\text{N}\) o dĺžku \(x_1 = 5 \,\text{cm}\). Aká práca sa vykoná pri predĺžení špirály na dvojnásobok jej pôvodnej dĺžky, keď sila konajúca prácu je úmerná predĺženiu špirály? [\(A = 128 \,\text{J}\)]

(110.) Drevený valec je ponorený vo vode do \( \tfrac{2}{3}\) svojej výšky. Akú prácu treba vykonať na vytiahnutie valca z vody, keď polomer valca je \(r = 10 \,\text{cm}\) a jeho výška \(h = 60 \,\text{cm}\)? [\(A = 24{,}1 \,\text{J}\)]

(115.) Ak na pružinu, ktorá sa nachádza vo zvislom puzdre, položíme guľôčku hmotnosti \(m = 0{,}1 \,\text{kg}\), stlačí sa pružina o \(\Delta s = 2 \,\text{mm}\). Do akej výšky vyletí guľôčka, keď pružinu stlačíme o \(s_1 = 15 \,\text{cm}\) a náhle uvoľníme? [\(h = \tfrac{s_1^2}{2 \Delta s} = 5{,}62 \,\text{m}\)]

(120.) Ako sa líši gravitačná sila, ktorou pôsobí Zem na telesá na zemskom povrchu v nadmorskej výške \(h = 6400 \,\text{m}\) a pri hladine mora (polomer Zeme \(R = 6378 \,\text{km}\))? [\(F_h = 0{,}998 F_0\)]

(121.) [4.23] Vypočítajte potenciál a intenzitu gravitačného poľa drôtu hmotnosti \(m\) ohnutého do tvaru kružnice s polomerom \(R\) v bode \(P\) na osi kružnice vo vzdialenosti \(a\) od jej stredu (obr. p121)!

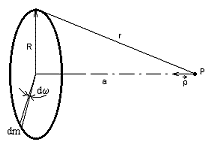Obr. p121

(122.) Nájdite zrýchlenie, ktorým by telesá padali na povrchu Mesiaca, ak predpokladáme, že na telesá pôsobí len gravitačné pole Mesiaca, a keď vieme, že hmotnosť a polomer Mesiaca sú \(M_M = \tfrac{1}{81} M_Z,\; R_M = \tfrac{1}{4} R_Z\), kde \(M_Z\) je hmotnosť Zeme a \(R_Z\) je polomer Zeme. [\(g_M = 0{,}2 g_Z = 1{,}962 \,\text{m·s}^{-2}\)]

(123.) Nájdite hodnotu rýchlosti \(v_0\), ktorú treba udeliť v smere zvislom nahor telesu nachádzajúcemu sa na povrchu Zeme, aby sa dostalo do výšky rovnajúcej sa zemskému polomeru, ktorý má hodnotu \(R = 6378 \,\text{km}\). (Odpor vzduchu zanedbajte.) [\(v_0 = 7{,}9 \,\text{km·s}^{-1}\)]

(152.) Nájdite polohu ťažiska útvaru znázorneného na obr. p152, ktorý vznikol tak, že sa z obdĺžnika so stranami \(a, b\) vyrezal na jednej jeho strane polkruh polomeru \(b/2\) a priložil sa na druhú stranu obdĺžnika.

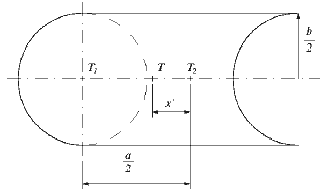
Obr. p152

(154.) Nájdite polohu ťažiska drôtu ohnutého do tvaru štvrťkružnice s polomerom \(R = 10 \,\text{cm}\).
[\(x^* = y^* = \tfrac{2R}{\pi} = 6{,}3 \,\text{cm}\), pričom začiatok súradnicovej sústavy je v strede kružnice a súradnicové osi sú polomery ohraničujúce štvrťkružnicu]

(159.) [3.30] Do telesa tvaru gule, zaveseného na vlákne, narazí vodorovne letiaci náboj, ktorého hmotnosť je 1000-krát menšia ako je hmotnosť telesa, a uviazne v tomto telese. Aká bola rýchlosť náboja pri náraze, keď sa teleso po náraze vychýlilo zo svojej rovnovážnej polohy tak, že záves zvieral so zvislým smerom uhol \(10^\circ\)? Dĺžka závesu od miesta upevnenia do stredu gule je \(l = 1 \,\text{m}\).
[\(v = 550 \,\text{m·s}^{-1}\)]

(161.) [5.17] O koľko treba predĺžiť homogénnu tyč dĺžky \(l = 0{,}75 \,\text{m}\), aby sa jej moment zotrvačnosti vzhľadom na os kolmú na tyč a prechádzajúcu ťažiskom tyče zdvojnásobil?
[pre \(m = \text{konšt.}\; \Delta l = 0{,}31 \,\text{m};\; \text{pre } S = \text{konšt.}\; \Delta l = 0{,}19 \,\text{m}\)]

(163.) [5.14] Nájdite moment zotrvačnosti rovnorodej dosky tvaru rovnoramenného trojuholníka s ramenami \(b\) a základňou \(2a\) vzhľadom na os kolmú na základňu a prechádzajúcu protiľahlým vrcholom, keď hmotnosť dosky je \(m\).
[\(I = \tfrac{1}{6} m a^2\)]

(169.) Homogénna kruhová doska s polomerom \(r = 0{,}3 \,\text{m}\) a hmotnosťou \(60 \,\text{kg}\) je pri svojom otáčavom pohybe okolo osi kolmej na rovinu dosky a prechádzajúcej stredom dosky vystavená účinku vonkajších síl, ktorých moment má konštantnú zložku do smeru osi otáčania hodnoty \(M = 0{,}1 \,\text{N·m}\). Vypočítajte uhlové zrýchlenie otáčavého pohybu dosky, ako aj prácu, ktorú vykonajú vonkajšie sily za prvé 3 minúty otáčania dosky, keď v čase \(t = 0 \,\text{s}\) bola doska v pokoji.
[\(\varepsilon = 0{,}037 \,\text{s}^{-2};\; A = 60 \,\text{J}\)]

(173.) Tyč dĺžky \(l = 1 \,\text{m}\) je upevnená tak, že sa môže otáčať okolo vodorovnej osi prechádzajúcej koncovým bodom tyče (obr. p173). Akú rýchlosť musíme udeliť voľnému koncovému bodu tyče, aby pri svojom vychýlení z rovnovážnej polohy dosiahol vodorovnú rovinu prechádzajúcu osou otáčania?

Obr. p173

[\(v_0 = \sqrt{3 g l} = 5{,}4 \,\text{m·s}^{-1}\)]

(191.) [12.7] O koľko by sa účinkom vlastnej tiaže predĺžilo oceľové lano dĺžky \(9000 \,\text{m}\) spustené do mora do takej hĺbky, aby lano voľne viselo a bolo celé ponorené do vody, ak hustota morskej vody je \(\rho_1 = 1{,}03 \cdot 10^3 \,\text{kg·m}^{-3}\), hustota lana je \(\rho_2 = 7{,}7 \cdot 10^3 \,\text{kg·m}^{-3}\) a modul pružnosti v ťahu ocele je \(E = 11{,}77 \cdot 10^{10} \,\text{Pa}\).
[\(\Delta l = 12{,}28 \,\text{m}\)]

(192.) [12.10] Valcová tyč pôvodnej dĺžky \(l_0\) je na jednom konci upevnená a na druhom konci namáhaná v smere dĺžky silou \(F\). Ako sa zmení objem tyče pri deformácii, keď modul pružnosti v ťahu materiálu tyče je \(E\)?
[\(\Delta V = \tfrac{l F (m - 2)}{m E}\)]

(195.) Drevená tyč s obdĺžnikovým prierezom so stranami \(a = 5 \,\text{cm},\; b = 0{,}5 \,\text{cm}\) je v dvoch miestach vzdialených od seba \(l = 1 \,\text{m}\) podopretá tak, že rozmer \(a\) je vo vodorovnej rovine. Ako sa zníži stred tyče vzhľadom na svoju pôvodnú polohu, keď tyč v strede zaťažíme závažím hmotnosti \(1 \,\text{kg}\), a keď modul pružnosti v ťahu dreva, z ktorého je tyč zhotovená, je \(E = 1{,}18 \cdot 10^{10} \,\text{Pa}\)?
[\(h = 3{,}33 \,\text{cm}\)]

(197.) Nájdite periódu torzného kyvadla, vytvoreného kruhovou doskou hmotnosti \(m = 3 \,\text{kg}\) a s polomerom \(R = 10 \,\text{cm}\) zavesenou na drôte dĺžky \(l = 1{,}2 \,\text{m}\) a polomeru \(r = 1 \,\text{mm}\), keď modul pružnosti ocele v šmyku je \(G = 7{,}16 \cdot 10^{10} \,\text{Pa}\).
[\(T = 2{,}51 \,\text{s}\)]

(219.) [7.31] V nádobe tvaru hranola je v bočnej stene kruhový otvor polomeru \(r = 20 \,\text{cm}\) uzavretý zátkou. Aká je celková sila, ktorá pôsobí na zátku, keď stred kruhového otvoru je vo výške \(h_1 = 50 \,\text{cm}\) nad dnom, a keď nádoba je naplnená vodou do výšky \(h = 1 \,\text{m}\)?
[\(F = \pi r^2 \rho g (h - h_1) = 616 \,\text{N}\)]

(220.) [7.2] Aká sila \(F\) je potrebná na zdvihnutie rovinnej hate, ktorá je pod tlakom vody (obr. p220), ak hmotnosť hate je \(m = 250 \,\text{kg}\), šírka hate \(b = 3 \,\text{m}\), hĺbka vody je \(h = 1{,}5 \,\text{m}\), a keď koeficient trenia hate o opory je \(\mu = 0{,}3\)?

Obr. p220

[\(F = 12\,390 \,\text{N}\)]

(226.) [7.29] Nádoba valcovitého tvaru má v stene nad sebou dva otvory vo výškach \(h_1\) a \(h_2\) od dna. V akej výške má byť hladina tekutiny nad dnom nádoby, aby tekutina striekala z obidvoch otvorov do rovnakej vzdialenosti na vodorovnú rovinu, na ktorej je nádoba položená?
[\(h = h_1 + h_2\)]

(229.) [7.23] Injekčná striekačka má plošný obsah piesta \(S_1 = 1{,}2 \,\text{cm}^2\) a jej otvor má prierez \(S_2 = 1 \,\text{mm}^2\). Ako dlho bude vytekať voda zo striekačky uloženej vo vodorovnej rovine, ak na piest bude pôsobiť sila \(F = 4{,}9 \,\text{N}\) a ak sa piest posunie celkom o dĺžku \(l = 4 \,\text{cm}\)? (Vnútorné trenie zanedbajte!)
[\(t = 0{,}53 \,\text{s}\)]

(254.) [3.18] Horizontálna doska koná harmonický pohyb vo vodorovnom smere s periódou \(T = 5 \,\text{s}\). Teleso, ktoré leží na doske, sa začína kĺzať, keď amplitúda kmitov dosiahne hodnotu \(x_0 = 0{,}5 \,\text{m}\). Aký je koeficient trenia medzi závažím a doskou?
[\(\mu = 0{,}08\)]

(256.) Na doske leží závažie hmotnosti \(m = 2 \,\text{kg}\). Doska koná harmonický pohyb vo zvislom smere s periódou \(T = 0{,}5 \,\text{s}\) a s amplitúdou \(x_0 = 3 \,\text{cm}\). Vyjadrite silu \(F\), ktorou závažie tlačí na dosku a vypočítajte amplitúdu tejto sily.
[\(F_\text{max} = 29 \,\text{N}\)]

(258.) Aký je koeficient útlmu tlmených harmonických kmitov hmotného bodu, keď podiel dvoch za sebou idúcich maximálnych výchyliek hmotného bodu na tú istú stranu sa rovná 2 a perióda tlmených kmitov je \(T = 0{,}5 \,\text{s}\)? Aká by bola perióda netlmených kmitov za rovnakých podmienok?
[\(b = 1{,}39 \,\text{s}^{-1};\; T_0 = 0{,}497 \,\text{s}\)]

(260.) [13.46] Nájdite amplitúdu výsledného harmonického pohybu, ktorý vznikne zložením dvoch jednosmerných kmitavých pohybov s rovnakou periódou, s amplitúdami \(3\) a \(5 \,\text{cm}\), keď rozdiel ich fáz je \(60^\circ\).
[\(x_0 = 7 \,\text{cm}\)]

(265.) Vypočítajte rýchlosť šírenia pozdĺžnych a priečnych vĺn v oceli s hustotou \(\rho = 7{,}8 \,\text{g·cm}^{-3}\), keď modul pružnosti v ťahu ocele je \(E = 20 \cdot 10^{10} \,\text{N·m}^{-2}\) a modul pružnosti v šmyku ocele je \(G = 8 \cdot 10^{10} \,\text{N·m}^{-2}\).
[\(v_l = 5065 \,\text{m·s}^{-1};\; v_p = 3200 \,\text{m·s}^{-1}\)]

(269.) Rušeň sa blíži k pozorovateľovi rýchlosťou \(v = 20 \,\text{m·s}^{-1}\). Aký vysoký základný tón píšťaly počuje pozorovateľ, ktorý je v pokoji, ak strojvodca počuje tón frekvencie \(f = 300 \,\text{s}^{-1}\) a ak rýchlosť zvuku vo vzduchu za daných podmienok je \(v_0 = 340 \,\text{m·s}^{-1}\)?
[\(f^* = 319 \,\text{s}^{-1}\)]

(285.) V tepelne izolovanej nádobe uvedieme do bezprostredného styku vodnú paru hmotnosti \(m_1\) a teploty \(t_1 = 100 \,^\circ\text{C}\), vodu hmotnosti \(m_0\) a teploty \(t_0\) a ľad hmotnosti \(m_2\) a teploty \(t_2 = 0 \,^\circ\text{C}\). Po určitom čase – po skvapalnení zložiek – sa v nádobe vytvorí kvapalina. Aká bude jej teplota? Špecifické skupenské teplo varu vody je \(l_1\), topenia ľadu \(l_2\) a špecifická tepelná kapacita vody je \(c\). Predpokladáme, že tepelnú kapacitu nádoby možno zanedbať.
[\(t = \frac{m_1 c t_1 + m_2 c t_2 + m_0 c t_0 + m_1 l_1 - m_2 l_2}{m_1 c - m_2 c + m_0 c}\)]

(291.) Homogénna železná tyč s hmotnosťou \(m = 3 \,\text{kg}\) má pri teplote \(8 \,^\circ\text{C}\) dĺžku \(1 \,\text{m}\). Vypočítajte, ako sa zmení moment zotrvačnosti tejto tyče vzhľadom na os kolmú na smer tyče a prechádzajúcu koncovým bodom, keď sa zohreje na teplotu \(100 \,^\circ\text{C}\).
[\(\Delta J = 22 \cdot 10^{-4} \,\text{kg·m}^2\)]

(297.) Sklenený pyknometer objemu \(V_0 = 15 \,\text{cm}^3\) je pri teplote \(t_0 = 0 \,^\circ\text{C}\) naplnený ortuťou. Keď teplotu okolia zvýšime na \(t_0 = 100 \,^\circ\text{C}\), z pyknometra vytečie \(\Delta V = 234 \,\text{mm}^3\) ortuti. Vypočítajte, aký je súčiniteľ objemovej rozťažnosti ortuti.
[\(\beta = 18{,}6 \cdot 10^{-5} \,\text{K}^{-1}\)]

(308.) V kalorimetri bolo \(1500 \,\text{g}\) vody o teplote \(6 \,^\circ\text{C}\), do ktorej sme pridali \(120 \,\text{g}\) ľadu neznámej teploty. Po vyrovnaní teplôt sme z vody kalorimetra ľad vybrali a zistili, že jeho hmotnosť sa zvýšila o \(12 \,\text{g}\). Aká bola pôvodná teplota ľadu?
[\(t = -166 \,^\circ\text{C}\)]

(337.) [8.12] Vypočítajte, koľko váži vzduch v miestnosti, ktorej rozmery sú: šírka \(4 \,\text{m}\), dĺžka \(5 \,\text{m}\), výška \(3 \,\text{m}\), pri tlaku \(0{,}1 \,\text{MPa}\) a pri izbovej teplote \(20 \,^\circ\text{C}\). Hustota vzduchu pri teplote \(0 \,^\circ\text{C}\) a tlaku \(0{,}1 \,\text{MPa}\) je \(1{,}293 \,\text{kg·m}^{-3}\).
[\(m = 72{,}3 \,\text{kg}\)]

(339.) [8.13] Žiarovka objemu \(150 \,\text{cm}^3\) je naplnená argónom. Aká je jeho teplota, keď pri tlaku \(0{,}1 \,\text{MPa}\) má argón tiaž \(1{,}42 \cdot 10^{-3} \,\text{N}\)?
[\(t = 224 \,^\circ\text{C}\)]

(348.) Vzduchová bublinka na dne jazera v hĺbke \(21 \,\text{m}\) má pri teplote \(t_1 = 4 \,^\circ\text{C}\) polomer \(r_1 = 1 \,\text{cm}\). Pomaly stúpa na povrch, pričom sa jej objem zväčšuje. Vypočítajte, aký bude jej polomer, keď dosiahne povrch jazera, ktorý má teplotu \(t_2 = 27 \,^\circ\text{C}\). Povrchové napätie neberte do úvahy. Atmosferický tlak \(b = 0{,}1 \,\text{MPa}\).
[\(r = 1{,}5 \,\text{cm}\)]

(349.) V jednom valci objemu \(V_1 = 5 \,\text{m}^3\) je kysličník uhoľnatý s tlakom \(p_1 = 15 \,\text{MPa}\), v druhom valci objemu \(V_2 = 8 \,\text{m}^3\) je vodík s tlakom \(p_2 = 22 \,\text{MPa}\) pri rovnakej teplote. Aký bude výsledný tlak zmesi po spojení oboch nádob? Teplota ostáva rovnaká.
[\(p = 19{,}3 \,\text{MPa}\)]

(403.) [9.23] Stroj pracujúci s výkonom \(P = 368 \,\text{W}\) vyvŕta za \(2 \,\text{minúty}\) otvor do liatinového bloku hmotnosti \(m = 20 \,\text{kg}\). O koľko stupňov sa blok ohreje, keď \(80 \%\) práce konanej pri vŕtaní prispieva k zväčšeniu vnútornej energie bloku? Merná tepelná kapacita liatiny je \(c = 544{,}2 \,\text{J·kg}^{-1}\text{·K}^{-1}\).
[\(\Delta t = 3{,}25 \,^\circ\text{C}\)]

(417.) Koľko tepla treba na izotermickú expanziu \(2 \,\text{litrov}\) vodíka tlaku \(0{,}08 \,\text{MPa}\) na štvornásobný objem? Aký bude výsledný tlak?
[\(Q = p_0 V_0 \ln\frac{V}{V_0};\; Q = 221{,}5 \,\text{J};\; p = 0{,}02 \,\text{MPa}\)]

(420.) [9.8] Kompresor nasáva atmosferický vzduch s tlakom \(0{,}01 \,\text{MPa}\) a teplotou \(27 \,^\circ\text{C}\) a stláča ho pri stálej teplote na tlak \(3{,}5 \,\text{MPa}\). Vypočítajte, koľko tepla sa odvádza chladiacej vode za hodinu, keď za tento čas sa stlačí \(10 \,\text{kg}\) vzduchu.
[\(Q = 3{,}1 \cdot 10^6 \,\text{J}\)]

(426.) [9.23] Určité množstvo vzduchu sme nechali rozopnúť zo začiatočného objemu \(V_0 = 2 \,\text{l}\) na päťnásobný. Začiatočný tlak vzduchu bol \(p_0 = 0{,}1 \,\text{MPa}\). Vypočítajte, akú prácu sme získali, keď sa expanzia uskutočnila:
a) izobaricky,
b) izotermicky,
c) adiabaticky.
[a) \(W = 7{,}8 \cdot 10^2 \,\text{J};\; b) W = 3{,}2 \cdot 10^2 \,\text{J};\; c) W = 2{,}3 \cdot 10^2 \,\text{J}\)]

(434.) [9.41] Aký najmenší musí byť výkon stroja, ktorý má odoberať vode stálej teploty \(t_1 = 17 \,^\circ\text{C}\) teplo \(Q = 41{,}9 \,\text{kJ·s}^{-1}\) a dodávať ho tepelnému radiátoru teploty \(t_2 = 46 \,^\circ\text{C}\)? Koľko tepla sa odovzdá vonkajšiemu zásobníku?
[\(P = 4{,}18 \,\text{kW};\; Q_1 = 46{,}1 \,\text{kJ·s}^{-1}\)]

(537.) V rohoch rovnostranného trojuholníka sú umiestnené rovnako veľké bodové náboje o veľkosti \(e\). Aký veľký bodový náboj máme umiestniť do stredu trojuholníka, aby boli náboje v rovnováhe?
[\(Q = 3^{-1/2} e\)]

(542.) Dva bodové náboje \(Q_1 = 8 \,\mu\text{C}\) a \(Q_2 = 5 \,\mu\text{C}\) sú vo vzdialenosti \(d = 20 \,\text{cm}\). Vypočítajte:
a) v ktorom mieste na ich spojnici sa intenzita elektrického poľa rovná nule,
b) v ktorom mieste na ich spojnici sú potenciály budené oboma nábojmi rovnaké.
[a) intenzita poľa je nulová vo vzdialenosti \(11{,}17 \,\text{cm}\) od väčšieho náboja;
b) potenciály sú rovnaké vo vzdialenosti \(12{,}31 \,\text{cm}\) od väčšieho náboja.]

(551.) Vypočítajte intenzitu elektrického poľa medzi dvoma súosými valcovými plochami s kruhovým prierezom s polomermi \(r_0\) a \(R_0\), prakticky nekonečne dlhými, keď vnútorný valec je nabitý na potenciál \(\varphi_0\) a vonkajší je uzemnený.
[\(E = \frac{\varphi_0}{r \ln \tfrac{R_0}{r_0}}\)]

(552.) Na vodiči ohnutom do tvaru kružnice polomeru \(R\) je uložený náboj \(Q\). Vypočítajte intenzitu elektrického poľa budeného týmto nábojom v strede kružnice, do ktorej je vodič ohnutý, ako aj v bode ležiacom na osi tejto kružnice vo vzdialenosti \(R\) od stredu tejto kružnice.
[\(E_1 = 0;\; E_2 = \tfrac{Q}{8 \pi \varepsilon_0 R^2 \sqrt{2}}\)]

(555.) Bod \(A\) sa nachádza vo vzdialenosti \(d\) od nekonečne veľkej vodivej roviny nabitej elektrickým nábojom s plošnou hustotou \(\sigma\) a obklopenej vákuom. Aký je potenciál elektrického poľa v bode \(A\) vzhľadom na uvedenú rovinu?
[\(\varphi = - \tfrac{\sigma d}{2 \varepsilon_0}\)]

(581.) Guľa polomeru \(R\), nabitá nábojom \(Q\), sa vyznačuje vo vákuu určitou potenciálnou energiou. Ako sa zmení potenciálna energia gule, keď ju ponoríme do tekutiny s relatívnou permitivitou \(\varepsilon_r\)?
[\(\Delta W = \tfrac{Q^2}{8 \pi \varepsilon_0 R} \, (1 - \varepsilon_r^{-1})\)]

(631.) Aký veľký odpor \(R_1\) musíme v zapojení na obr. 1 nastaviť kontaktom na odpore \(R = 10 \,\Omega\), aby galvanometrom \(G\) neprechádzal prúd? Elektromotorické napätia sú \(U_{e1} = 20 \,\text{V}\) a \(U_{e2} = 12 \,\text{V}\).

Obr. p631
[\(R_1 = 6 \,\Omega\)]

(638.) Aký veľký úbytok napätia \(\Delta U\) vzniká v dvojitom medenom vedení prierezu \(S = 10 \,\text{mm}^2\), ktorým sa prenáša prúd \(I = 5 \,\text{A}\) do vzdialenosti \(s = 500 \,\text{m}\) do zdroja s napätím \(U = 220 \,\text{V}\), a aké veľké je napätie na svorkách spotrebiča?
[\(U = 8{,}5 \,\text{V};\; U_s = 211{,}5 \,\text{V}\)]

(640.) Keď spojíme voltmeter do série s odporom \(R = 10^4 \,\Omega\), a keď ho pripojíme k zdroju napätia \(U_e = 120 \,\text{V}\), ukáže napätie \(U_1 = 50 \,\text{V}\). Keď spojíme voltmeter do série s neznámym odporom \(R_x\), ukáže pri rovnakom napätí zdroja napätie \(U_2 = 10 \,\text{V}\). Vypočítajte veľkosť neznámeho odporu \(R_x\).
[\(R_x = 78\,600 \,\Omega\)]

(643.) Tri galvanické články s elektromotorickými napätiami \(U_{e1} = 1{,}3 \,\text{V},\; U_{e2} = 1{,}5 \,\text{V},\; U_{e3} = 2 \,\text{V}\) majú vnútorné odpory \(R_1 = R_2 = R_3 = 0{,}2 \,\Omega\) a sú zapojené podľa obr. 2. Odpor \(R = 0{,}55 \,\Omega\). Určte prúdy \(I_1, I_2, I_3\).

Obr. p643
[\(I_1 = 4 \,\text{A};\; I_2 = 1{,}5 \,\text{A};\; I_3 = 2{,}5 \,\text{A}\)]

(646.) Miliampérmeter so stupnicou \(d = 100\) dielikov, s vnútorným odporom \(R = 10 \,\Omega\), pre \(I' = 10 \,\text{mA}\) sa má použiť:
a) ako voltmeter do \(U = 300 \,\text{V}\),
b) ako ampérmeter do \(I = 20 \,\text{A}\).
Aký bude potrebný predradený odpor, resp. bočník?
[a) \(r = 29\,990 \,\Omega;\; b) r' = \tfrac{10}{1999} \,\Omega\)]

(648.) Voltmeter s vnútorným odporom \(3000 \,\Omega\) má rozsah do \(150 \,\text{V}\) a stupnicu rozdelenú na \(150\) dielikov. Aký prúd tečie voltmetrom pri plnej výchylke a aký predradený odpor musíme zapojiť, aby sa rozsah prístroja zväčšil na \(600 \,\text{V}\)? Aké napätie bude prislúchať dieliku stupnice?
[\(I = 0{,}05 \,\text{A};\; r = 9000 \,\Omega;\; 4 \,\text{V}\)]

(654.) Aký veľký výkon musí mať elektrický varič, aby zohrial \(2 \,\text{litre}\) vody o teplote \(10^\circ \text{C}\) na teplotu \(100^\circ \text{C}\) za \(25 \,\text{minút}\), keď sa na ohrievanie využije len \(70\%\) varičom vyvinutého tepla?
[\(P = 717{,}6 \,\text{W}\)]

(655.) Aký musí byť odpor spotrebiča, aby v ňom za každú hodinu vzniklo \(3684 \,\text{kJ}\) tepla pri napätí \(220 \,\text{V}\)?
[\(R = 46{,}7 \,\Omega\)]

(701.) Veľmi dlhý priamy vodič, ktorým tečie prúd \(I = 10 \,\text{A}\), vytvára v určitom mieste kruhový závit s polomerom \(R = 4{,}28 \,\text{cm}\) ležiaci tak, že normála na rovinu závitu je kolmá na priamu časť vodiča (obr. 3). Vypočítajte smer a veľkosť indukcie magnetického poľa v strede kruhového závitu.

Obr. p701
[\(\cotg \,\alpha = \pi,\; \alpha = 17^\circ 40'\), kde \(\alpha\) je uhol medzi rovinou kruhového závitu a \(B\); \(B = \tfrac{\mu_0 I}{2 \pi R} \cdot \sqrt{1 + \pi^2} = 1{,}54 \cdot 10^{-4} \,\text{T}\)]

(703.) Vypočítajte intenzitu magnetického poľa vyvolaného úsekom priameho vodiča, ktorým preteká prúd \(I = 10 \,\text{A}\), v bode nachádzajúcom sa vo vzdialenosti \(5 \,\text{cm}\) kolmo od stredu tohto úseku vodiča. Dĺžka vodiča je taká, že ju vidieť z bodu, v ktorom intenzitu počítame, pod zorným uhlom \(60^\circ\). Prostredie okolo vodiča je vákuum.
[\(H = 15{,}9 \,\text{A·m}^{-1}\); smer je kolmý na rovinu preloženú uvažovaným bodom a vodičom]

(709.) Dva veľmi dlhé priame rovnobežné vodiče sú od seba vzdialené \(d = 10 \,\text{cm}\). Prúdy tečúce vodičmi, \(I_1 = 10 \,\text{A}\) a \(I_2 = 20 \,\text{A}\), majú rovnaký smer. Vypočítajte veľkosť a smer intenzity magnetického poľa v rovine vodičov, a to v strede medzi vodičmi.
[\(H = 63{,}69 \,\text{A·m}^{-1}\); smer \(H\) je kolmý na rovinu preloženú vodičmi]

(714.) Akou silou sa priťahujú dva rovnobežné vodiče, z ktorých jeden je veľmi dlhý a preteká ním prúd \(I_1 = 250 \,\text{A}\), druhý má dĺžku \(s = 20 \,\text{cm}\) a preteká ním prúd \(I_2 = 300 \,\text{A}\), keď vzájomná vzdialenosť oboch vodičov je \(a = 1 \,\text{cm}\) a vodiče sú umiestnené vo vákuu?
[\(F = 0{,}3 \,\text{N}\)]

(719.) V homogénnom magnetickom poli indukcie \(B = 2 \,\text{T}\) sa pohybuje rýchlosťou \(v = 10 \,\text{m·s}^{-1}\) kolmo na indukčné čiary vodič s ohmickým odporom \(R_v = 0{,}1 \,\Omega\) a dĺžkou \(l = 30 \,\text{cm}\). Konce vodiča sú pripojené na odpor \(R = 0{,}4 \,\Omega\). Vypočítajte, aký výkon je potrebný na pohyb vodiča.
[\(P = 72 \,\text{W}\)]

(727.) V homogénnom magnetickom poli s indukciou \(B = 0{,}2 \,\text{T}\) sa v rovine kolmej na \(B\) rovnomerne otáča vodivá tyč dĺžky \(l = 10 \,\text{cm}\). Os otáčania je kolmá na tyč a prechádza koncovým bodom tyče. Vypočítajte frekvenciu otáčania tyče, keď sa v nej indukuje elektromotorické napätie veľkosti \(U_i = 0{,}628 \,\text{V}\).
[\(f = \tfrac{U_i}{\pi B l^2} = 102 \,\text{s}^{-1}\)]

(735.) Dva priame veľmi dlhé rovnobežné vodiče sa nachádzajú v určitej vzdialenosti od seba. Vodičmi pretekajú prúdy \(I_1 = 40 \,\text{A}\) a \(I_2 = 30 \,\text{A}\) v rovnakých smeroch. Na zväčšenie vzájomnej vzdialenosti vodičov na trojnásobok treba vykonať určitú prácu. Vypočítajte časť tejto práce, ktorá pripadá na jednotkovú dĺžku vodiča!
[\(W = 26{,}3 \cdot 10^{-5} \,\text{J·m}^{-1}\)]

(783.) Sériový obvod zložený z kondenzátora kapacity \(C = 8 \,\mu\text{F}\) a cievky s indukčnosťou \(L = 2 \,\text{H}\) a s ohmickým odporom \(R = 30 \,\Omega\) je pripojený k zdroju s napätím \(U = 110 \,\text{V}\) a frekvenciou \(f = 50 \,\text{s}^{-1}\). Určte impedanciu celého obvodu, prúd v obvode, napätie na kondenzátore a cievke a účinník obvodu!
[\(Z = 232 \,\Omega;\; I = 0{,}47 \,\text{A};\; U_C = 187 \,\text{V};\; U_L = 295 \,\text{V};\; \cos \varphi = 0{,}129\)]

(787.) Cievkou s indukčnosťou \(L = 0{,}25 \,\text{H}\) tečie prúd \(I = I_0 \sin \omega t\), kde \(I_0 = 1 \,\text{A}\) a \(\omega = 3140 \,\text{s}^{-1}\). Nájdite maximálnu hodnotu indukovaného elektromotorického napätia, ktoré sa v cievke indukuje!
[\(U_0 = 785 \,\text{V}\)]

(793.) Elektromagnetický oscilátor je zdrojom elektromagnetických vĺn s frekvenciou \(f = 300 \,\text{MHz}\). Nájdite vlnovú dĺžku elektromagnetických vĺn, keď prostredie, ktorým sa šíria, má relatívnu permitivitu \(\varepsilon_r = 25\) a relatívnu permeabilitu \(\mu_r = 1\).
[\(\lambda = 0{,}2 \,\text{m}\)]

(848.) V akej výške nad vodorovnou rovinou je oblak, ktorý pozorujeme zo skaly vysokej \(h = 76 \,\text{m}\) vo výškovom uhle \(\alpha = 56^\circ\) a jeho obraz na vodnej hladine jazera pri skale v hĺbkovom uhle \(58^\circ\)?
[\(x = 2000 \,\text{m}\)]

(864.) Spojná šošovka vytvorí obraz svietiaceho zdroja na tienidle vo vzdialenosti \(l = 1 \,\text{m}\) od zdroja. Ak šošovku posunieme do druhej polohy, pričom polohu zdroja a tienidla už nemeníme, na tienidle sa znova vytvorí svetelný obraz zdroja. Aká je ohnisková vzdialenosť šošovky, keď na vytvorenie druhého jasného obrazu zdroja treba šošovku posunúť k tienidlu o vzdialenosť \(d = 20 \,\text{cm}\)?
[\(f = 24 \,\text{cm}\)]

(895.) Biele svetlo sa odráža kolmo na plochách vzdušnej vrstvy hrubej \(1 \,\mu\text{m}\), ktorá sa nachádza medzi dvoma sklenými doskami. Určte vlnové dĺžky svetla vo viditeľnej oblasti, ktoré sú v odrazenom svetle najviac a) zosilnené, b) zoslabené.
[a) \(571{,}4 \,\text{nm};\; 444 \,\text{nm};\;\; b) \; 666{,}6 \,\text{nm};\; 500 \,\text{nm};\; 400 \,\text{nm}\)]

(896.) Na veľmi tenkú sklenú doštičku tvaru klina dopadá kolmo na jej povrch rovnobežný zväzok monofrekvenčných lúčov s vlnovou dĺžkou \(\lambda = 0{,}5 \,\mu\text{m}\). Interferenčný úkaz v doštičke pozorujeme v odrazenom svetle. Vypočítajte uhol, ktorý zvierajú plochy klína, keď vzdialenosť susedných tmavých pásikov je \(5{,}6 \,\text{nm}\)!
[\(\varphi = 6''\)]

(902.) Úzka štrbina je osvetlená rovnobežným zväzkom bieleho svetla, dopadajúceho kolmo na štrbinu. Určte, pre ktorú vlnovú dĺžku splynie stred tretieho tmavého pásika so stredom druhého tmavého pásika pre červenú farbu vlnovej dĺžky \(\lambda_\text{č} = 690 \,\text{nm}\).
[\(\lambda = 460 \,\text{nm},\; \text{pre modrú farbu}\)]

(906.) Röntgenové lúče dopadajú na rovinnú stenu kryštálu NaCl a odrážajú sa pod uhlom \(\alpha = 5{,}9^\circ\), meranom od tejto roviny v prvom ráde \((k = 1)\). Aká je vlnová dĺžka dopadajúceho žiarenia? Hustota NaCl je \(2170 \,\text{kg·m}^{-3}\).
[\(\lambda = 0{,}058 \,\text{nm}\)]

(957.) Koľko fotónov vyšle za sekundu svetelný zdroj monofrekvenčného svetla o vlnovej dĺžke \(\lambda = 560 \,\text{nm}\), keď celková energia fotónov vyslaných za sekundu je \(1{,}5 \cdot 10^{-3} \,\text{J}\)?
[\(n = 4{,}24 \cdot 10^{15}\)]

(960.) Akú kinetickú energiu má protón, keď jemu prislúchajúca vlnová dĺžka de Broglieho vĺn \(\lambda = 9{,}04 \cdot 10^{-13} \,\text{m}\)?
[\(W_k = 103 \,\text{eV}\)]

(961.) Určte energiu, hybnosť a hmotnosť fotónu \(\gamma\)-žiarenia s vlnovou dĺžkou \(\lambda = 10^{-12} \,\text{m}\).
[\(W_k = 1{,}978 \cdot 10^{-13} \,\text{J};\; p = 6{,}624 \cdot 10^{-22} \,\text{kg·m·s}^{-1};\; m = 2{,}21 \cdot 10^{-30} \,\text{kg}\)]

(967.) Fotón röntgenového žiarenia s frekvenciou \(1{,}5 \cdot 10^{19} \,\text{s}^{-1}\) bude mať po zrážke s elektrónom frekvenciu \(1{,}2 \cdot 10^{19} \,\text{s}^{-1}\). Akú bude mať elektrón energiu po zrážke?
[\(W_e = 83{,}9 \cdot 10^{-15} \,\text{J}\)]

(968.) Súradnicu polohy \(x\) čiastočky prachu hmotnosti \(m = 10^{-15} \,\text{kg}\) sme určili s nepresnosťou \(\Delta x = 10^{-8} \,\text{m}\). Nájdite nepresnosť v určení súradnice jej rýchlosti \(\Delta v_x\)!
[\(\Delta v_x \geq 10^{-11} \,\text{m·s}^{-1}\)]

(984.) Aká je perióda obiehania elektrónu po tretej kvantovej dráhe v Bohrovom modeli atómu vodíka?
[\(T_3 = 4{,}1 \cdot 10^{-15} \,\text{s}\)]

(985.) Vypočítajte vlnové dĺžky prvých troch čiar Balmerovej série vodíkového spektra! \((R_\infty = 1{,}097373 \cdot 10^{7} \,\text{m}^{-1})\)
[\(\lambda_1 = 0{,}656 \,\mu\text{m};\; \lambda_2 = 0{,}486 \,\mu\text{m};\; \lambda_3 = 0{,}434 \,\mu\text{m}\)]

(1005.) Konečným produktom rádioaktívneho rozpadu \(^{232}_{90}\text{Th}\) je izotop \(^{208}_{82}\text{Pb}\). Vypočítajte, koľko častíc \(\alpha\) a koľko častíc \(\beta\) sa uvoľní pri tomto rozpade!
[6; 4]

(1006.) Vypočítajte, za aký čas sa rozpadne polovica atómov rádia, keď jeho rozpadová konštanta \(\lambda = 1{,}42 \cdot 10^{-11} \,\text{s}^{-1}\)!
[\(T = 1550 \,\text{rokov}\)]

(1007.) Vypočítajte, koľko percent určitého množstva rádioaktívneho polónia s polčasom rozpadu 40 minút sa rozpadne za 5 minút!
[\(p = 8{,}3 \,\%\)]

(1019.) Vypočítajte väzbovú energiu jadra izotopu a) \(^{14}_{7}\text{N}\), b) \(^{208}_{82}\text{Pb}\). Aká stredná energia pripadá na jeden nukleón? Relatívna atómová hmotnosť izotopu \(^{14}_{7}\text{N}\) je \(14{,}00756 \,u\) a \(^{208}_{82}\text{Pb}\) \(207{,}21 \,u\).
[a) \(\Delta W_1 = 104{,}4 \,\text{MeV};\; b) \Delta W_2 = 1467{,}9 \,\text{MeV};\; \Delta W_s = 7{,}1 \,\text{MeV}\)]