Rozpad rádioaktívneho polónia – Fyzika v príkladoch

Rádioaktivita je schopnosť niektorých jadier samovoľne sa rozpadať a pritom vyžarovať neviditeľné žiarenie. Rozpad prirodzene rádioaktívnych jadier prebieha samovoľne, pričom úbytok nerozpadnutých rádioaktívnych atómov môžeme popísať zákonom prirodzeného úbytku:

\[
dn = - \lambda n \, dt \tag{1}
\]

ktorý hovorí, že ak rádioaktívna látka v čase \(t\) obsahovala \(n\) nerozpadnutých atómov, za čas \(dt\) sa ich rozpadne \(dn\), kde \(\lambda\) je rozpadová konštanta danej rádioaktívnej látky. Počet ešte nerozpadnutých atómov rádioaktívnej látky v čase \(dt\) je teda určený exponenciálnym zákonom v integrálnom tvare:

\[
n = n_0 \, e^{-\lambda t} \tag{2}
\]

kde \(n_0\) je počiatočné množstvo atómov v čase \(t = 0 \,\text{s}\). Čas, za ktorý sa rozpadne polovica počiatočného množstva atómov \(n = \tfrac{n_0}{2}\) sa nazýva polčas rozpadu \(T\). Platí teda:

\[
\frac{n_0}{2} = n_0 e^{-\lambda T} \quad \text{resp. } e^{\lambda T} = 2 \tag{3}
\]

Odtiaľ pre polčas rozpadu \(T\) dostávame:

\[
T = \frac{\ln 2}{\lambda} \tag{4}
\]

Percentuálny počet množstva polónia, ktoré sa rozpadne za čas \(t\) určíme zo vzťahu:

\[
p = 1 - \frac{n}{n_0} \tag{5}
\]

kde \(\tfrac{n}{n_0}\) predstavuje percentuálny počet ešte nerozpadnutého množstva rádioaktívnej látky. Úpravou predchádzajúcich vzťahov pre hľadané rozpadnuté množstvo polónia dostaneme:

\[
p = 1 - e^{-\lambda t}
\]

\[
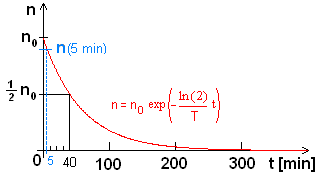
p = 1 - e^{-\tfrac{\ln 2}{T} \, t}
\]

Dosadením zadaných hodnôt dostávame:

\[
p = 1 - e^{-\tfrac{0.693 \cdot 5 \,\text{min}}{40 \,\text{min}}}
\]

\[
p = 8.3 \,\%
\]

Za 5 minút sa rozpadne \(8.3 \,\%\) určitého množstva rádioaktívneho polónia.