Riešené príklady > Magnetizmus

793. Elektromagnetický oscilátor je zdrojom elektromagnetických vĺn s frekvenciou \( f = 300 \ \text{MHz} \). Nájdite vlnovú dĺžku elektromagnetických vĺn, keď prostredie, ktorým sa šíria, má relatívnu permitivitu \( \varepsilon_r = 25 \) a relatívnu permeabilitu \( \mu_r = 1 \)!

\( f = 300 \ \text{MHz}, \)
\( \varepsilon_r = 25, \)
\( \mu_r = 1, \)
\( \lambda = \ ? \)

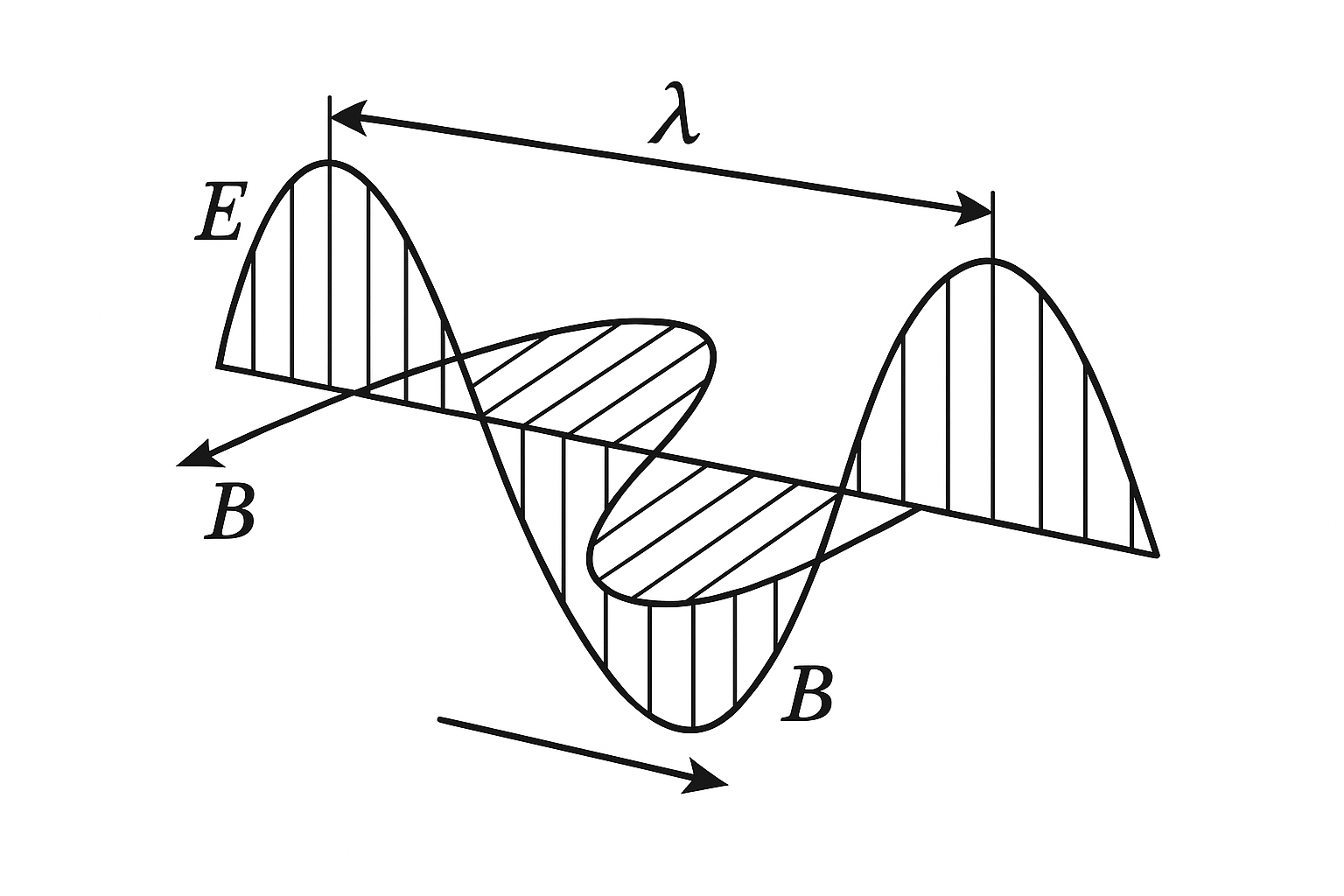
Existenciu elektromagnetických vĺn potvrdzujú Maxwellove rovnice. Na opis týchto vĺn používame analogické veličiny ako u mechanických vĺn, čiže vlnovú dĺžku \( \lambda \), frekvenciu \( f \), periódu \( T \), ktorých súvis s rýchlosťou \( v \) šírenia sa vĺn je rovnaký ako u mechanických veličín:

\[ \lambda = vT = \frac{v}{f} \tag{1} \]

Z porovnania všeobecnej vlnovej rovnice:

\[ \frac{\partial^2 \vec{u}}{\partial t^2} = v^2 \, \Delta \vec{u} \tag{2} \]

kde \( u \) je výchylka z rovnovážnej polohy a \( v \) je rýchlosť šírenia sa vĺn v danom prostredí, s diferenciálnymi rovnicami elektromagnetického vlnenia pre elektrický vzruch:

\[ \frac{\partial^2 \vec{E}}{\partial t^2} = \frac{1}{\varepsilon_0 \varepsilon_r \mu_0 \mu_r} \, \Delta \vec{E} \tag{3} \]

kde \( E \) je vektor intenzity elektrického poľa, resp. pre magnetický vzruch (\( B \) je vektor magnetickej indukcie):

\[ \frac{\partial^2 \vec{B}}{\partial t^2} = \frac{1}{\varepsilon_0 \varepsilon_r \mu_0 \mu_r} \, \Delta \vec{B} \tag{4} \]

vyplýva, že rýchlosť šírenia sa elektromagnetického vzruchu v nevodivom prostredí je:

\[ v = \frac{1}{\sqrt{\varepsilon_0 \varepsilon_r \mu_0 \mu_r}} \tag{5} \]

Pre hľadanú vlnovú dĺžku teda platí:

\[ \lambda = \frac{v}{f} = \frac{1}{f \sqrt{\varepsilon_0 \varepsilon_r \mu_0 \mu_r}} \] \[ \lambda = \frac{1}{300 \cdot 10^{6} \ \text{Hz} \, \sqrt{8{,}854 \cdot 10^{-12} \ \text{A}^2 \text{kg}^{-1} \text{m}^{-3} \text{s}^4 \cdot 4\pi \cdot 10^{-7} \ \text{A}^{-2} \text{kg} \text{m} \text{s}^{-2}}} \] \[ \lambda = 0{,}2 \ \text{m} \tag{6} \]

Vlnová dĺžka elektromagnetických vĺn je 0,2 metra.