Riešené príklady > Magnetizmus

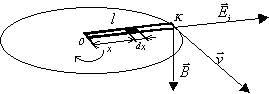
727. V homogénnom magnetickom poli s indukciou \( B = 0{,}2 \ \text{T} \) sa v rovine kolmej na \( B \) rovnomerne otáča vodivá tyč dĺžky \( l = 10 \ \text{cm} \). Os otáčania je kolmá na tyč a prechádza koncovým bodom tyče. Vypočítajte frekvenciu otáčania tyče, keď sa v nej indukuje elektromotorické napätie \( U_i = 0{,}628 \ \text{V} \).

\( B = 0{,}2 \ \text{T}, \)
\( l = 0{,}1 \ \text{m} \)
\( U_i = 0{,}628 \ \text{V}, \)
\( f = \ ? \)

Odhliadnuc od neusporiadaných termických pohybov častíc v tyči môžeme povedať, že kladné ióny aj voľné elektróny sú v relatívnom pokoji vzhľadom na tyč, avšak vzhľadom k okoliu sú unášané istou obvodovou rýchlosťou. Na tieto náboje v neuzavretom vodiči pohybujúcom sa v magnetickom poli pôsobí Lorentzova sila: \[ F = q (\vec{v} \times \vec{B}) \tag{1} \] Účinkom ktorej sa voľné elektróny budú pohybovať. (Pre ióny \( q > 0 \) a pre elektróny \( q < 0 \).) Tieto nabité častice sa teda chovajú tak, ako keby v pohybujúcej sa tyči pôsobilo elektrické pole intenzity \( \vec{E}_i \):

\[ \vec{E}_i = \frac{\vec{F}_m}{q} = \vec{v} \times \vec{B} \tag{2} \]

ktorú nazývame indukovaná elektromotorická intenzita. Pole \( \vec{E}_i \) nemôže narušiť rovnomerné rozloženie kladných iónov viazaných na kryštálovú mriežku kovu, ale spôsobí nerovnomerné rozloženie záporných voľných elektrónov. Časť elektrónov sa vo veľmi krátkom čase presunie k jednému koncu vodiča – osi otáčania a vytvorené pole kompenzuje indukovanú intenzitu \( \vec{E}_i \). Tyčou však nebude tiecť trvalý prúd, ale vodič sa nabije presne na napätie, ktoré sa rovná indukovanému. Pre napätie, ktoré by sme mohli namerať medzi začiatkom \( 0 \) a koncom tyče \( K \) platí:

\[ U_i = \int_{0}^{K} \vec{E}_i \cdot d\vec{l} = \int_{0}^{K} (\vec{v} \times \vec{B}) \cdot d\vec{l} = - \int_{0}^{K} \vec{B} \cdot (\vec{v} \times d\vec{l}) = - \int_{0}^{K} \vec{B} \cdot \frac{d\vec{S}}{dt} \tag{3} \]

Vektorový súčin \( (\vec{v} \times \vec{B}) \) má smer rovnobežný s vektorom \( d\vec{l} \), ktorý je orientovaný od \( 0 \) do \( K \). Preto je integrál z \( \vec{E}_i \) od \( 0 \) do \( K \) kladný, \( U_i \) medzi \( 0 \) a \( K \) je tiež kladné, má teda orientáciu od pólu – k pólu + cez zdroj, ktorý je v tomto prípade tyč. Pole \( \vec{E}_i \) však nie je potenciálové, ale vírové. V prípade priameho vodiča dĺžky \( l \), ktorý sa pohybuje kolmo na indukčné čiary (vektor \( \vec{B} \) je kolmý na plochu \( d\vec{S} \) – rovnobežný s jej vektorom \( d\vec{S} \)), dostaneme:

\[ U_i = (\vec{v} \times \vec{B}) \cdot \vec{l} = - (\vec{B} \times \vec{v}) \cdot \vec{l} = - B v l = - \frac{B \, dS}{dt} = - \frac{d\varphi}{dt} \tag{4} \]

pričom \( d\Phi \) má význam toku vektora magnetickej indukcie cez plochu \( dS \), ktorú dĺžka \( l \) pretne za čas \( dt \). Zo vzťahu (4) vidieť, že vo vodiči dĺžky \( x \) pohybujúcom sa rýchlosťou \( v \) v homogénnom magnetickom poli kolmo na magnetickú indukciu \( B \), sa indukuje elektromotorické napätie, ktorého veľkosť je daná vzťahom:

\[ |U_i| = B \, x \, v \tag{5} \]

Element vodiča dĺžky \( dx \), vo vzdialenosti \( x \) od osi otáčania sa pohybuje rýchlosťou, ktorá sa rovná obvodovej rýchlosti kruhového pohybu elementu, t. j.:

\[ v = 2 \pi f x \tag{6} \]

kde \( f \) je frekvencia otáčania tyče. Veľkosť elektromotorického napätia indukovaného v danom elemente \( dx \) bude:

\[ |dU_i| = B v \, dx = B \, 2 \pi f x \, dx \tag{7} \]

V celom vodiči dĺžky \( l \) sa indukuje elektromotorické napätie veľkosti:

\[ |U_i| = 2 \pi f B \int_{0}^{l} x \, dx = f B l^{2} \pi \tag{8} \]

Hľadanú frekvenciu \( f \) získame úpravou predchádzajúceho vzťahu:

\[ f = \frac{|U_i|}{B l^{2} \pi} \tag{9} \]

Dosadením číselných hodnôt dostaneme:

\[ f = \frac{0{,}628 \ \text{V}}{0{,}2 \ \text{T} \cdot 0{,}1^{2} \ \text{m}^{2} \pi} \] \[ f = 10^{2} \ \text{Hz} \]

Frekvencia otáčania tyče v homogénnom magnetickom poli je \( f = 10^{2} \ \text{Hz} \).