Riešené príklady > Stavba látok

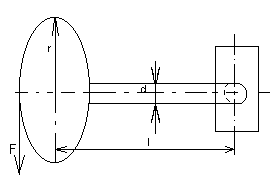
185. Železná valcová tyč dĺžky \( l = 50\ \mathrm{cm} \) a priemeru \( d = 0{,}5\ \mathrm{cm} \) je na jednom konci upevnená.
Na jej druhom konci je upevnené koleso polomerom \( r = 20\ \mathrm{cm} \).
Akou tangenciálnou silou treba pôsobiť na obvode kolesa, aby sa prierez tyče v mieste kolesa stočil vzhľadom na upevnený koniec tyče o uhol \( \varphi = 15^\circ \), keď modul pružnosti v torzii železa \( G = 7{,}16 \cdot 10^{10}\ \mathrm{Pa} \)?

\( l = 50\ \mathrm{cm} \)

\( d = 0{,}5\ \mathrm{cm} \)

\( r = 20\ \mathrm{cm} \)

\( \varphi = 15^\circ \)

\( G = 7{,}16 \cdot 10^{10}\ \mathrm{Pa} \)

\( F =\ ? \)

Medzi uhlom otočenia kolesa \( \varphi \) a momentom síl \( M \), ktoré spôsobujú skrútenie tyče, je priama úmera. V oblasti platnosti Hookovho zákona je vzťah medzi momentom \( M \) a pootočením \( \varphi \) jednej základne voči druhej nasledovný:

\[ M = \frac{ \pi G \left(\frac{d}{2}\right)^4 \varphi }{2l} \tag{1} \]

Moment sily sa v prípade tangenciálnej sily \( F \) vyjadrí:

\[ M = Fr \tag{2} \]

takže pre hľadanú silu \( F \) platí:

\[ F = \frac{ \pi G d^4 \varphi }{32 l r} \tag{3} \]

\[ F = \frac{ 3{,}14 \cdot 7{,}16 \cdot 10^{10}\ \mathrm{N/m^2} \cdot 625 \cdot 10^{-12}\ \mathrm{m^4} }{32 \cdot 0{,}5\ \mathrm{m} \cdot 0{,}2\ \mathrm{m}} \cdot \frac{15 \pi}{180} \]

\[ F = 11{,}1\ \mathrm{N} \]

Aby sa prierez tyče v mieste kolesa stočil vzhľadom na upevnený koniec tyče o uhol \( \varphi \), treba na obvode kolesa pôsobiť tangenciálnou silou \( 11{,}1\ \mathrm{N} \).