Riešené príklady > Gravitačné pole
Potenciál a intenzita gravitačného poľa
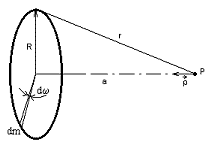
121. Vypočítajte potenciál a intenzitu gravitačného poľa drôtu hmotnosti \(m\), ohnutého do tvaru kružnice s polomerom \(R\), v bode \(P\) na osi kružnice vo vzdialenosti \(a\) od jej stredu (obr.)!
Kružnicu s polomerom \(R\) si môžeme rozdeliť na jednotlivé elementy, pričom každý element hmotnosti \(dm\) má od bodu \(P\) rovnakú vzdialenosť \(r\), ktorú vypočítame podľa Pytagorovej vety:
\[ r = (R^2 + a^2)^{1/2} \tag{1} \]
Každému elementu s hmotnosťou \(dm\) prislúcha element obvodu kružnice \(do\), pre ktorý platí:
\[ do = R \, d\omega \tag{2} \]
kde \(\omega\) je z intervalu \(\langle 0, 2\pi \rangle\). Pre veľkosť elementu hmotnosti \(dm\) môžeme teda písať:
\[ dm = \frac{m}{O} \, do = \frac{m}{2\pi R} \, do \tag{3} \]
kde \(O\) predstavuje obvod drôtu (kružnice) \((O = 2\pi R)\). Element drôtu \(dm\), vybraný v podobe úseku drôtu dĺžky \(do\), prispieva k celkovému potenciálu \(\varphi\) v bode \(P\) hodnotou:
\[ d\varphi = - \kappa \cdot \frac{1}{r} \, dm \tag{4} \] \[ d\varphi = - \kappa \left[ \frac{m}{2\pi R} \cdot \frac{1}{(R^2 + a^2)^{1/2}} \right] \, do \tag{5} \]
Celkový potenciál gravitačného poľa drôtu \(\varphi\) v bode \(P\) dostaneme integrovaním cez celý obvod kružnice:
\[ \varphi = - \kappa \left[ \frac{m}{2\pi R} \cdot \frac{1}{(R^2 + a^2)^{1/2}} \right] \int_0^{2\pi R} do \] \[ \varphi = - \kappa \left[ \left( \frac{m}{2\pi R} \cdot \frac{1}{(R^2 + a^2)^{1/2}} \right) \cdot 2\pi R \right] \] \[ \varphi = - \kappa \cdot \frac{m}{(R^2 + a^2)^{1/2}} \tag{6} \]
Medzi vektorom intenzity \(K\) a potenciálom \(\varphi\) v ľubovoľnom mieste gravitačného poľa platí vzťah:
\[ K = - \text{grad} \, \varphi \tag{7} \]
kde \(\text{grad} \, \varphi\) predstavuje zmenu potenciálu v smere \(a\):
\[ K = - \frac{d\varphi}{da} = \frac{d\varphi}{da} \, \rho \tag{8} \] \[ K = \left[ - \kappa m (R^2 + a^2)^{-1/2} \right]' \, \rho \] \[ K = \kappa m \cdot \frac{1}{2} (R^2 + a^2)^{-3/2} \cdot 2a \, \rho \] \[ K = \kappa m a (R^2 + a^2)^{-3/2} \, \rho \tag{9} \]
Intenzita gravitačného poľa drôtu je \( K = \kappa m a (R^2 + a^2)^{-3/2} \, \rho \).