Riešené príklady > Gravitačné pole

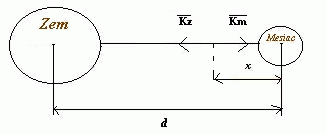
86. V ktorom mieste na priamej spojnici medzi Zemou a Mesiacom sa intenzita spoločného gravitačného poľa rovná nule, keď vieme, že hmotnosť Mesiaca je \(\frac{1}{81}\) hmotnosti Zeme?

\[ M_m = \frac{1}{81} M_z \] \[ x = \, ? \]

Hľadáme miesto, v ktorom bude platiť, že veľkosť vektora intenzity gravitačného poľa Zeme \(K_z\) je rovná veľkosti vektora intenzity gravitačného poľa Mesiaca \(K_m\). Z gravitačného zákona vyplýva:

\[ |K_z| = |K_m| \] \[ k \cdot \frac{M_z}{(d - x)^2} = k \cdot \frac{M_m}{x^2} \] \[ \frac{M_z}{(d - x)^2} = \frac{1}{81} \cdot \frac{M_z}{x^2} \] \[ x^2 = \frac{(d - x)^2}{81} \] \[ x = \frac{d - x}{9} \] \[ 9x = d - x \] \[ 10x = d \] \[ x = \frac{d}{10} \]

Nulová intenzita spoločného gravitačného poľa Zeme a Mesiaca na spojnici ich stredov je vo vzdialenosti \(\frac{1}{10}\) ich spoločnej vzdialenosti od stredu Mesiaca.