Riešené príklady > Dynamika

110. Drevený valec je ponorený vo vode do \(\frac{2}{3}\) svojej výšky. Akú prácu treba vykonať na vytiahnutie valca z vody, keď polomer valca \(r = 10 \, \text{cm}\) a jeho výška \(h = 60 \, \text{cm}\)?

\(l = \frac{2}{3} h\)
\(h = 60 \, \text{cm}\)
\(r = 10 \, \text{cm}\)
\(A = \, ?\)

Práca ako dráhový účinok sily je definovaná vzťahom:

\[ A = \int_{x_1}^{x_2} \vec{F}(x) \cdot d\vec{x} \tag{1} \]

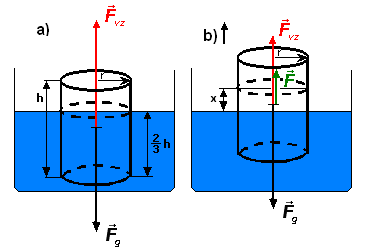
kde \(\vec{x}_1\) je polohový vektor začiatočného bodu a \(\vec{x}_2\) je polohový vektor koncového bodu dráhy, po ktorej sa pohybuje pôsobisko sily \(\vec{F}\). Pri ponorení dreveného valca do kvapaliny sa valec ustáli, keď tiažová sila Zeme \(\vec{F}_G\) pôsobiaca na valec bude v rovnováhe s hydrostatickou vztlakovou silou \(\vec{F}_{\text{vz}}\) (obr. a)). Pri povytiahnutí valca z kvapaliny sa rovnováha týchto síl poruší, keďže sa zmenší vztlaková sila kvapaliny v dôsledku zmenšeného objemu ponorenej časti valca. Aby sa valec nepohyboval v smere výslednej sily nadol a aby sme ho mohli vytiahnuť z kvapaliny von, musíme naň pôsobiť prinajmenšom silou rovnou úbytku vztlakovej sily (obr. b)), teda:

\[ \vec{F}(x) = V \, \rho_k \, g = S x \, \rho_k \, g \tag{2} \]

kde \(x\) predstavuje dráhu, o ktorú sme valec povytiahli z kvapaliny von. Celková práca, ktorú vykonáme pri vytiahnutí valca von z kvapaliny, teda pri posunutí o \(\frac{2}{3} h\), je rovná:

\[ A = \int_{0}^{\frac{2}{3}h} \vec{F}(x) \cdot d\vec{x} = \int_{0}^{\frac{2}{3}h} S x \, \rho_k g \, dx = \pi r^2 \, \rho_k g \left[ \frac{x^2}{2} \right]_0^{\frac{2}{3}h} \tag{3} \]

Po dosadení číselných hodnôt dostaneme:

\[
W = 3{,}14 \cdot 0{,}1^2 \, \text{m}^2 \cdot 1000 \, \text{kg/m}^3 \cdot 9{,}81 \, \text{m/s}^2 \cdot \left( \frac{ \frac{4}{9} \cdot 0{,}6^2 }{2} \right) \, \text{m}^2
\]

\[ W = 24,7 J \]

Na vytiahnutie valca z vody treba vynaložiť prácu \(24{,}7 \, \text{J}\).