Riešené príklady > Kinematika

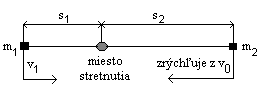
Dve telesá vzdialené od seba na začiatku \(100 \, \text{m}\) sa pohybujú proti sebe – prvé rovnomerne s rýchlosťou \(v_1 = 3 \, \text{m/s}\), druhé rovnomerne zrýchlene s počiatočnou rýchlosťou \(v_0 = 7 \, \text{m/s}\) a so zrýchlením \(a = 4 \, \text{m/s}^2\).
Nájdite miesto a čas ich stretnutia.

\(s = 100 \, \text{m}\),
\(t_0 = 0 \, \text{s}\),
\(v_1 = 3 \,
\text{m/s}\),
\(v_0 = 7 \, \text{m/s}\),
\(a = 4 \, \text{m/s}^2\),
\(s_1 = ?\), \(t = ?\)

Telesá sa pohybujú proti sebe. Pre ich vzdialenosť \(s\) platí:

\[ s = s_1 + s_2 \tag{1} \]

Vieme, že sa začali pohybovať v tom istom čase \(t_0 = 0 \, \text{s}\). Prvé z telies sa pohybuje pomalšie ako druhé, z čoho môžeme usudzovať, že sa stretnú bližšie k prvému z telies. Vieme, že prvé z telies sa pohybuje rýchlosťou \(v_1 = 3 \, \text{m/s}\) rovnomerným pohybom istý čas \(t\). Pre jeho dráhu \(s_1\) teda platí:

\[ s_1 = v_1 t \tag{2} \]

Druhé z telies sa pohybuje pohybom, ktorý je rovnomerne zrýchlený. Jeho počiatočná rýchlosť je \(v_0 = 7 \, \text{m/s}\) a v čase \(t_0 = 0 \, \text{s}\) sa toto teleso začalo pohybovať proti prvému so zrýchlením \(a = 4 \, \text{m/s}^2\). Tento pohyb trval, takisto ako v prvom prípade, istý čas \(t\). Pre jeho dráhu \(s_2\) teda platí:

\[ s_2 = v_0 t + \frac{1}{2} a t^2 \tag{3} \]

Dosadením do vzťahu (1) dostaneme:

\[ s = s_1 + s_2 = v_1 t + v_0 t + \frac{1}{2} a t^2 \tag{4} \]

Úpravou a dosadením zadaných hodnôt získame kvadratickú rovnicu, z ktorej si vypočítame čas:

\[ s = v_1 t + v_0 t + \frac{1}{2} a t^2 \] \[ s = t(v_1 + v_0) + \frac{1}{2} a t^2 \] \[ 100 = 10t + 2t^2 \] \[ t^2 + 5t - 50 = 0 \] \[ t_1 = 5 \, \text{s}, \quad t_2 = -10 \, \text{s} \]

Keďže neuvažujeme záporný čas, \(t_2\) neberieme do úvahy.

Vzdialenosť od prvého telesa dostaneme po dosadení času \(t = 5 \, \text{s}\) do vzťahu pre \(s_1\):

\[ s_1 = v_1 t \] \[ s_1 = 3 \, \text{m/s} \cdot 5 \, \text{s} \] \[ s_1 = 15 \, \text{m} \]

Telesá sa stretnú za čas \(5\) sekúnd vo vzdialenosti \(15\) metrov od prvého z nich.